Adaptive Logics Home Page
[Back]
Bibliography
BiBfile
Centre for Logic and Philosophy of Science
This file was not updated for quite a while. In compensation, several parts of the upcoming book are available. To see them, click here.
This page is meant as an introduction to adaptive logics and as a working instrument for those familiar with it. References are to the adaptive logic Bibliography, which contains some abstracts and notes, and which is linked to the BiBfile. Those wandering may return safely to the right spot in the present file by clicking the [Back] buttons. For footnotes, click on the superscripted number in the text to read the note, and on the superscripted number in the note to return to the text.
Most unpublished papers may be downloaded from the writings list of the Centre. For additions and corrections, please send a message to Diderik.Batens@UGent.be
Contents
Introduction
The adaptive logic programme aims at developing a type of formal logics (and the connected metatheory) that is especially suited to explicate the many interesting dynamic consequence relations that occur in human reasoning but for which there is no positive test (see the next section). Such consequence relations occur, for example, in inductive reasoning, handling inconsistent data, ...
The explication of such consequence relations is realized by the dynamic proof theories of adaptive logics. These proof theories are dynamic in that formulas derived at some stage may not be derived at a later stage, and vice versa.
The programme is application driven. This is one of the reasons why the predicative level is
considered extremely important, even if, for many adaptive logics, the basic features of the
dynamics are already present at the propositional level. The main applications are taken from the philosophy of science; some also from more pedestrian contexts.
The interest in dynamic consequence relations led rather naturally to an interest in dynamic aspects of reasoning. Some of these already occur in Classical Logic (henceforth CL).
Some survey papers: [Bat00c], [Bat04b] and [Bat01b].
The problem
Much interesting actual reasoning displays two forms of non-standard dynamics.
|
1
|
An external dynamics: a conclusion may be withdrawn in view of new information. This means that the consequence relation is non-monotonic.[1]
|
|
2
|
An internal dynamics: a conclusion may be withdrawn in view of the better understanding of the premises provided by a continuation of the reasoning.
|
While examples of logics displaying the external dynamics are available, logicians did not pay much attention to the internal dynamics. And yet it is very familiar to anyone. Reasoning from one’s convictions, one often derives a consequence that one later rejects, even if one’s convictions were not modified. The point is that humans are unable to see at once all the consequences of a set of premises (in this case, one’s convictions).
It is a mistake to think that the internal dynamics only occurs if the consequence relation is non-monotonic (and hence is affected by the external dynamics). Indeed, the Weak consequence relation, a Rescher-Manor consequence relation (see below), is monotonic. Nevertheless, any proof theory that characterizes the Weak consequence relation is affected by the internal dynamics. (See [Bat00d], [Bat03b] and [BV02].) And in [Bat01a] it is shown that the pure calculus of relevant implication, which is decidable, may be characterized by a proof theory that displays the internal dynamics.
To clearly understand the two forms of dynamics, it is useful to compare them to the standard forms of logical dynamics. These are common to all reasoning, and well known from usual logics. First consider the standard external dynamics. If we are reasoning (by some logic L) from a set of data  and, at some point in time, are supplied with a supplementary set of data
and, at some point in time, are supplied with a supplementary set of data  ', we are in general able to derive more consequences from that point in time on. Formally: CnL(
', we are in general able to derive more consequences from that point in time on. Formally: CnL( )
) 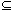 CnL(
CnL(
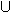
 ’).[2]
Next consider the standard internal dynamics. Given a set of rules of inference, not all formulas derivable from a set of premises are derivable by a single application of a rule at some stage of a proof. The set of formulas derivable by a single application of a rule monotonically increases as the proof proceeds. A different form of dynamics is related to the fact that humans are unable to see at once all the consequences of a set of premises. As a result, some statements will only be seen to be derivable from the premises after other statements have been derived. The derivability of a statement, however, does not depend on the question whether one sees that it is derivable. So, this form of internal dynamics is related to logical heuristics and to computational aspects, rather than of the logic properly. To be more precise: the formulation of the proof theory is fully independent of it. As we shall see later, the matter is completely different for consequence relations that display an adaptive internal dynamics.
’).[2]
Next consider the standard internal dynamics. Given a set of rules of inference, not all formulas derivable from a set of premises are derivable by a single application of a rule at some stage of a proof. The set of formulas derivable by a single application of a rule monotonically increases as the proof proceeds. A different form of dynamics is related to the fact that humans are unable to see at once all the consequences of a set of premises. As a result, some statements will only be seen to be derivable from the premises after other statements have been derived. The derivability of a statement, however, does not depend on the question whether one sees that it is derivable. So, this form of internal dynamics is related to logical heuristics and to computational aspects, rather than of the logic properly. To be more precise: the formulation of the proof theory is fully independent of it. As we shall see later, the matter is completely different for consequence relations that display an adaptive internal dynamics.
Many consequence relations are undecidable[3] and the predicative versions of nearly all logics are undecidable. If a logic is undecidable but monotonic, there still may be a positive test for derivability.[4] However, if a consequence relation is undecidable and non-monotonic, there can only be a positive test for it in some rather artificial cases.[5] There may at best be a definition of consequence relation in terms of a monotonic logic or in terms of a semantics or in terms of continuations of a proof. And as a logic may be decidable for certain fragments of the language, there may also be criteria for derivability.
For this reason, we shall need a special kind of proofs to explicate the consequence relations we are considering. Here adaptive logics and their dynamic proof theories come in. We shall also need to develop several new metatheoretic tools in order to obtain a decent formal control on adaptive logics.
-------
Notes (click on the number to return to the text)
|
[1]
|
A consequence relation  is non-monotonic iff (if and only if) there is a formula A and there are sets of formulas is non-monotonic iff (if and only if) there is a formula A and there are sets of formulas  and and  ', such that ', such that   A whereas A whereas  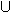  ' ' 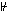 A (A is a consequence of A (A is a consequence of  , but not of , but not of  together with together with  '). ').
|
|
[2]
|
CnL( ) = {A | ) = {A |   L A} (the set of all formulas derivable from L A} (the set of all formulas derivable from  by L). by L).
|
|
[3]
|
A logic is decidable iff there is an algorithm to find out, for any finite set of premises and for any formula, whether the formula is derivable from the premises. (See also the following note.)
|
|
[4]
|
There is a positive test for derivability iff there is an algorithm that leads, for any set of premises and for any formula, to the answer “Yes” in case the formula is derivable from the premises. CL-derivability is decidable for the propositional fragment of CL and undecidable for full (predicative) CL. Still, there is a positive test for CL-derivability. A standard reference for such matters is [BJ89].
|
|
[5]
|
For most sensible non-monotonic consequence relations  L, there are monotonic consequence relations L, there are monotonic consequence relations  L1 and L1 and  L2 such that L2 such that   L A iff L A iff   L1 B and L1 B and 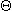 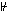 L2 C, in which there are certain relations between L2 C, in which there are certain relations between  , ,  and and 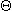 on the one hand (these sets may all be identical) and between A, B and C on the other hand (A and B may be identical and C may be ~A), and in which on the one hand (these sets may all be identical) and between A, B and C on the other hand (A and B may be identical and C may be ~A), and in which  L1 and L1 and  L2 may be identical. If the latter two are undecidable, then even if there is a positive test for them and even if the relations between the sets and formulas are decidable, there is no positive test for L2 may be identical. If the latter two are undecidable, then even if there is a positive test for them and even if the relations between the sets and formulas are decidable, there is no positive test for  L. L.
|
Characterization of an adaptive logic
A general characteristic of the consequence relations mentioned in the previous section is that certain inferences are considered as correct iff certain formulas behave normally. What normality means will depend on the adaptive logic. In an inconsistency-adaptive logic, abnormalities are inconsistencies (possibly of a specific form); in some adaptive logics of induction, abnormalities are negations of generalizations (for example: ~(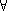 x)(Px
x)(Px Qx)). In some (prioritized) adaptive logics, abnormalities (of some priority level) are negations of premises (of that priority) -- see the section on Flat and prioritized adaptive logics for an example.[1]
Qx)). In some (prioritized) adaptive logics, abnormalities (of some priority level) are negations of premises (of that priority) -- see the section on Flat and prioritized adaptive logics for an example.[1]
An adaptive logic supposes that all formulas behave normally unless and until proven otherwise. Moreover, if an abnormality occurs, it is considered as local. This means that, even if some formula behaves abnormally, all other formulas are still supposed to behave normally unless and until proven otherwise. We shall see the effect of this in the following section.
While some consequences of a set of premises depend on the normal behaviour of certain formulas, other consequences follow come what may. Thus, an adaptive logic of induction enables one to derive certain generalizations as well as certain ‘predictions’ from a set of premises. To do so, one relies on the supposition that formulas behave normally unless and until proven otherwise. However, the premises also have deductive consequences that follow independently of any normality suppositions.
This naturally leads to seeing an adaptive logic as defined by three elements: the lower limit logic, a set of abnormalities, and an adaptive strategy.
· The lower limit logic determines which consequences hold independently of any presuppositions (or conditions).
· A set of abnormalities, which is characterized by a logical form. For example, the set of abnormalities may contain the existential closure of all formulas of the form A&~A. This logical form may be restricted. For example, the formulas of the form A&~A may be restricted to those in which A is a primitive formula (a schematic letter for sentences, a primitive predicative formula, or an identity). Extending the lower limit logic with an axiom that rules out the occurrence of abnormalities, results in the upper limit logic. In other words, the set of lower limit models[2] that verify no abnormality are the upper limit models. The upper limit logic determines which consequences follow in the normal situation.
· An adaptive strategy. If an abnormality is derivable from the premises (by the lower limit logic), the upper limit logic reduces the premises (or theory) to triviality.[3] However, the adaptive logic still interprets the premises “as normally as possible”. This phrase is ambiguous: there are several ways to do so. The adaptive strategy will pick one specific way to interpret the premises as normally as possible.
This clarifies the way in which adaptive logics adapt themselves to specific premises. The logic interprets the premises in agreement with the lower limit logic and, moreover, as much as possible in agreement with the upper limit logic. If some formulas (premises or lower limit consequences of the premises) are abnormal, the adaptive logic will not add the upper limit consequences of these formulas. For all other formulas, the upper limit logic consequences are added. I further clarify this in the subsequent section.
-------
Note (click on the number to return to the text)
|
[1]
|
In most adaptive logics, abnormalities are formulas of a specific logical form -- contradictions, negations of universally quantified formulas, etc. In some ampliative adaptive logics, however, abnormalities (at some priority level) are negations of premises of that priority level. The abnormalities may have any logical form and no logical form warrants abnormality.
|
|
[2]
|
I write “lower limit models” rather than “models of the lower limit logic”. Similarly for other such expressions.
|
|
[3]
|
A consequence set is trivial if it contains all statements (all formulas of the language schema). Thus CL assigns the trivial consequence set to all inconsistent sets of premises because it validates Ex Falso Quodlibet: A, ~A  B. That a logic assigns the trivial consequence set to some set of premises means that, in semantic terms, the set of premises has no models or that its only model is the trivial one. (The second disjunct needs to be added because some semantic systems contain trivial models.) B. That a logic assigns the trivial consequence set to some set of premises means that, in semantic terms, the set of premises has no models or that its only model is the trivial one. (The second disjunct needs to be added because some semantic systems contain trivial models.)
|
Corrective and ampliative adaptive logics
What are corrective adaptive logics? [Back]
The original type of research on adaptive logics concerned the following type of problem. Suppose that a scientific (empirical or mathematical) theory was meant to be consistent and was formulated with CL as its underlying logic, but turned out to be inconsistent. As we know from the literature, scientists do not just throw away such theories to start from scratch. They reason from the inconsistent theory in search for a consistent replacement.
This reasoning cannot proceed in terms of CL because the CL-consequence set of an inconsistent theory is trivial. But it also cannot proceed in terms of a monotonic paraconsistent logic[1] because such logics assign to the theory a consequence set that is too weak (see the next two paragraphs). On our way to a replacement for the inconsistent theory, we want to interpret it as much as possible in agreement with its intended interpretation, in other words, as consistently as possible.
Monotonic paraconsistent logics offer too weak an interpretation of the theory because they invalidate some rules of CL. For example, CL validates Disjunctive Syllogism: A B, ~A
B, ~A  B, whereas most[2] paraconsistent logics don’t. It is easy to understand why they don’t. CL presupposes that A and ~A are not both true, and that a disjunction is true iff at least one of its disjuncts is true. So, ~A and A
B, whereas most[2] paraconsistent logics don’t. It is easy to understand why they don’t. CL presupposes that A and ~A are not both true, and that a disjunction is true iff at least one of its disjuncts is true. So, ~A and A B can only be true together if B is true. Paraconsistent logics do not exclude that A and ~A are both true. And whenever A and ~A are both true, ~A and A
B can only be true together if B is true. Paraconsistent logics do not exclude that A and ~A are both true. And whenever A and ~A are both true, ~A and A B are true, even if B is false.[3]
B are true, even if B is false.[3]
That (monotonic) paraconsistent logics invalidate rules of CL makes them unfit for solving the problem from the first paragraph. Let us consider a simple example (actually, an unrealistically simple one). Suppose that the ‘theory’ {~p, p q, ~r, r
q, ~r, r s, p} was intended as consistent and was given CL as its underlying logic. Finding out that it is inconsistent, we want to interpret it as much as possible according to the original intention. Clearly, we do not want to derive q from the first two premises. p
s, p} was intended as consistent and was given CL as its underlying logic. Finding out that it is inconsistent, we want to interpret it as much as possible according to the original intention. Clearly, we do not want to derive q from the first two premises. p q is a consequence of p. Applying Disjunctive Syllogism to additive consequences of p and ~p leads to triviality. However, no problem arises if we apply Disjunctive Syllogism to ~r and r
q is a consequence of p. Applying Disjunctive Syllogism to additive consequences of p and ~p leads to triviality. However, no problem arises if we apply Disjunctive Syllogism to ~r and r s, and hence conclude to s. As we want to interpret the premises as consistently as possible, we must consider s as a consequence of the premises. Inconsistency-adaptive logics do precisely this. According to them, B is a consequence of ~A and A
s, and hence conclude to s. As we want to interpret the premises as consistently as possible, we must consider s as a consequence of the premises. Inconsistency-adaptive logics do precisely this. According to them, B is a consequence of ~A and A B iff A behaves normally (which here means: consistently) on the premises. In our example, r behaves normally whereas p does not.[4]
B iff A behaves normally (which here means: consistently) on the premises. In our example, r behaves normally whereas p does not.[4]
Inconsistency-adaptive logics are corrective: they interpret a set of premises as much as possible in agreement with the intended standard of deduction. There are many other corrective adaptive logics. Indeed, we should not be obsessed by inconsistency, which is a glut with respect to negation (both A and ~A are true for some A). There are many other logical abnormalities: gaps with respect to negation, (neither A nor ~A is true for some A), and gluts and gaps with respect to other logical constants (conjunction, implication, quantifiers, identity). All logics that allow for such gluts or gaps (or both), but interpret the premises as much as possible in agreement with the intended standard of deduction, are corrective adaptive logics. (See [Bat97] for the arguments and [Bat99e] or [Bat01c] for the logics). A very different kind of corrective adaptive logics are ambiguity-adaptive logics (see [Van97] or [Van99]; see also [Bat02c]).
What are ampliative adaptive logics? [Back]
While corrective adaptive logics were being studied, it was found that many adaptive logics are ampliative in that they assign to a set of premises a consequence set that extends the consequence set assigned to the premises by the standard of deduction (usually again CL). For example, the adaptive logic of induction allows one to derive not only CL-consequences from some set of data (and from some background knowledge), but allows one also to derive generalizations and predictions that are not CL-consequences.
Originally, we tried to develop a separate terminology for ampliative adaptive logics. Soon this turned out to be useless and even counterproductive. The main reason for this is that both kinds of adaptive logics have the same basic structure. In fact, the distinction between them is not a systematic one, but is based on a non-logical criterion: the choice of a standard of deduction. If, for example, the chosen standard of deduction is CL, adaptive logics are corrective if they have CL as their upper limit logic, and are ampliative if they have CL as their lower limit logic.
Remark that the same adaptive logic may be corrective for the one and ampliative for the other. A nice illustration is provided by Priest’s LPm from [Pri91]. This inconsistency-adaptive logic has the monotonic paraconsistent logic LP as its lower limit logic and CL as its upper limit logic. For people that consider CL as the standard of deduction, it is a corrective adaptive logic. Priest, however, who is a dialetheist,[5] considers LP as the standard of deduction. For him, LPm is an ampliative adaptive logic.
Some adaptive logics are both corrective and ampliative. For example, a realistic adaptive logic of induction should not only extend the CL-consequences of the premises, but should also be able to handle inconsistent background theories.
As the distinction is pragmatically useful, it is followed in the present text. But it is good to remember that the distinction is merely pragmatically useful and hence largely conventional.
Effects on the search for the logic [Back]
First consider corrective adaptive logics. Here the upper limit logic is given (the standard of deduction). The problem is to handle theories that share a specific type of abnormality with respect to the upper limit logic (and hence are reduced to triviality by this logic). (It is wise to identify the type of abnormality in a precise way, and to consider different conceptualizations; see also the next section). The first task is to find a lower limit logic. This should be a fragment of the upper limit logic that allows for the abnormalities under consideration. In other words, the lower limit logic is obtained from the upper limit logic by removing a specific presupposition from the latter. For example, each of the following are presuppositions of CL: that ~A is false if A is true, that A&B is true if both A and B are true, that different occurrences of a non-logical symbol have always the same meaning,[6] etc. The next task is to choose a strategy that is suitable for the specific application context. Given this, a rather standard sequence of steps leads to the dynamic proof theory and to the semantics.
The matter is somewhat more complicated for ampliative adaptive logics because here the lower limit logic is given. Of course, we shall have an idea of the supplementary consequences that we want to be derivable in specific cases. But we still have to find an upper limit logic and a set of abnormalities with respect to this upper limit logic. These should be such that the upper limit models coincide with the lower limit models that do not verify any abnormality. The heuristically most efficient way to proceed is usually to start from the dynamic proof theory. This often offers a clue on the conditions (see the section on the dynamic proof theory) that govern the derivation of the supplementary formulas. These conditions determine the abnormalities of the (known) lower limit logic with respect to the (unknown) upper limit logic. Once the abnormalities are delineated, one readily finds the upper limit logic. From there on, a rather standard sequence of steps will again lead to the full logic.
-------
Note (click on the number to return to the text)
|
[1]
|
A logic is paraconsistent iff it does not validate A, ~A  B (Ex Falso Quodlibet), in other words, if it does not assign the trivial consequence set to all inconsistent sets of premises. B (Ex Falso Quodlibet), in other words, if it does not assign the trivial consequence set to all inconsistent sets of premises.
|
|
[2]
|
See [Meh00b] for an interesting exception.
|
|
[3]
|
This shows that Disjunctive Syllogism is invalid in paraconsistent logics in which disjunction behaves in the standard way. Moreover, adding Disjunctive Syllogism to such paraconsistent logics ruins their paraconsistent character. Indeed, any formula is derivable from A and ~A by the joint application of Addition and Disjunctive Syllogism: from A follows A B (Addition), and from this together with ~A follows B (Disjunctive Syllogism). In the sequel of this section, I only consider logics that validate Addition. B (Addition), and from this together with ~A follows B (Disjunctive Syllogism). In the sequel of this section, I only consider logics that validate Addition.
|
|
[4]
|
In this simple example, we had only to consider the question whether some premises behave consistently. However, the adaptive derivability of a formula from a set of premises depends in general on the question whether some formulas (which need not be premises) behave consistently with respect to the set of premises. This consistent or inconsistent behaviour is determined by the set of premises together with the lower limit logic. An example is discussed in the section on Strategies.
|
|
[5]
|
Dialetheists believe that there are true inconsistencies. Not all paraconsistent logicians are dialetheists. Databases may be inconsistent because the information contained in them provides from different sources. Our knowledge may be inconsistent because it is defective or provides from fallible methods and tools. Paraconsistent logicians have widely diverging views as far as the truth of inconsistencies is concerned. Some are dialetheists, some believe that all inconsistencies are false, some are agnostic on the matter.
For a dialetheist, an inconsistency-adaptive logic mainly serves the purpose to explain why most of classical reasoning is correct, even if (according to the dialetheist) it is not correct for logical reasons but because consistency may be presupposed unless and until proven otherwise.
|
|
[6]
|
This gives us A  A, which typically is not generally correct in the presence of ambiguities. A, which typically is not generally correct in the presence of ambiguities.
|
Normality: some examples
Example 1: inconsistency.
A simple example was given in the subsection defining corrective adaptive logics. In general, abnormalities are formulas of the form
|
(1)
|
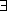 (A&~A) (A&~A)
|
in which 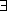 abbreviates an existential quantifier over any variable free in A. In the propositional case, this reduces to formulas of the form A&~A.
In some adaptive logics, all formulas of form (1) count as abnormalities. This holds specifically if the lower limit logic does not enable one to reduce complex inconsistencies to disjunctions or conjunctions of simpler ones. The first inconsistency-adaptive logics, which had CLuN as their lower limit logic, were of this kind.
abbreviates an existential quantifier over any variable free in A. In the propositional case, this reduces to formulas of the form A&~A.
In some adaptive logics, all formulas of form (1) count as abnormalities. This holds specifically if the lower limit logic does not enable one to reduce complex inconsistencies to disjunctions or conjunctions of simpler ones. The first inconsistency-adaptive logics, which had CLuN as their lower limit logic, were of this kind.
The matter is different if the lower limit logic reduces complex abnormalities. Thus, if the lower limit logic is CLuNs, (p&~p) (q&~q) is derivable from (p&q)&~(p&q) because ~(A&B)
(q&~q) is derivable from (p&q)&~(p&q) because ~(A&B)  CLuNs ~A
CLuNs ~A ~B. In such cases, not all formulas of the form (1) should be counted as abnormalities. To be more precise, in adaptive logics that have CLuNs as their lower limit logic, a formula of the form (1) is counted as an abnormality iff A is a primitive formula (a schematic letter for sentences, a primitive predicative formula, or an identity).[1] If, in such cases, all formulas of the form
~B. In such cases, not all formulas of the form (1) should be counted as abnormalities. To be more precise, in adaptive logics that have CLuNs as their lower limit logic, a formula of the form (1) is counted as an abnormality iff A is a primitive formula (a schematic letter for sentences, a primitive predicative formula, or an identity).[1] If, in such cases, all formulas of the form 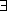 (A&~A) are counted as abnormalities, then one obtains an adaptive logic that is inadequate. This may best be explained in a short excursion.
(A&~A) are counted as abnormalities, then one obtains an adaptive logic that is inadequate. This may best be explained in a short excursion.
Excursion: flip-flop logics.
If CLuNs is the lower limit logic and all formulas of the form (1) are considered as abnormalities, then one obtains the following result:
|
(i)
|
If the premises are consistent, the adaptive consequences coincide with the CL-consequences.
|
|
(ii)
|
If the premises are inconsistent, the adaptive consequences coincide with the CLuNs-consequences.
|
The name flip-flop logic refers to the fact that this adaptive logic simply selects one of two monotonic logics, depending on a property of the set of premises. While (i) is all right, (ii) is not. Even if the premises are inconsistent, we want the inconsistency-adaptive logic to interpret them as consistently as possible. While this flip-flop logic is an adaptive logic, it should be stressed that the usual and more interesting adaptive logics are not flip-flop logics.
Example 2: Gluts with respect to the universal quantifier.
Formulas of the form (1) are gluts with respect to negation: if A is a closed formula, both A and ~A are true. A gap with respect to negation occurs where both A and ~A are false. There may be gluts and/or gaps with respect to other logical constants.
A glut with respect to the universal quantifier occurs when a universally quantified formula is true whereas some of its instances are false. For example: (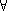 x)(Px
x)(Px Qx) and Pa are true but Qa is false. In this case an abnormality is a formula of the form
Qx) and Pa are true but Qa is false. In this case an abnormality is a formula of the form
|
(2)
|
(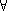 x)(A(x))&~A(a) for some a. x)(A(x))&~A(a) for some a.
|
in which x is a metavariable for individual variables and a is a metavariable for individual constants. Formulas of the form (2) are abnormalities with respect to CL. In some adaptive logics that handle such gluts all formulas of the form (2) are abnormalities, in other adaptive logics only a subset of formulas of the form (2) count as abnormalities.
An adaptive logic that handles gluts with respect to the universal quantifier will interpret sets of premises as expected: it does not lead from formulas of the form (2) to triviality, but presupposes such formulas to be false unless and until proven otherwise. In other words, it will interpret a set of premises as normally as possible (with respect to this type of abnormalities).
Here are some obvious application contexts for this type of corrective adaptive logics: default rules (handling such statements as ‘Birds fly’), generalizations that are falsified but are nevertheless applied (because they lead to correct results in most cases), etc. We shall see that such cases may also be handled by ampliative adaptive logics. Which adaptive logic should be applied depends on the context.
Example 3: ambiguity.
When we interpret a text, we presuppose that all occurrences of the same word have the same meaning throughout the text. Sometimes, it appears from the text that different occurrences of the same word must have different meanings. This appears because, if all those occurrences had the same meaning, then the author of the text would be stating a (clearly not intended) contradiction.[2]
If we distinguish different occurrences of a word by superscripts, ~(p1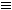 p2) expresses an abnormality of the sentential letter p, ~a4=a17 an abnormality for the individual constant a, etc. Remark that, on this approach, any schematic letter (but no other formula) may behave abnormally.
p2) expresses an abnormality of the sentential letter p, ~a4=a17 an abnormality for the individual constant a, etc. Remark that, on this approach, any schematic letter (but no other formula) may behave abnormally.
An ambiguity-adaptive logic interprets a text as normally as possible. It interprets all occurrences of a word as having the same meaning, unless and until this appears to be impossible. Remark again that abnormalities are local. Even if the occurrences of a word have different meanings in the text, the logic will still presuppose that other words behave normally.[3]
Example 4: induction.
Inductive reasoning relies on the supposition that there is a certain regularity (in the world, and hence) in our experiences. Of course, one does not start from scratch, but relies on a set of background knowledge, which is the result of the inductive reasoning of our predecessors. As a result, we need at least two standards of normality.
Background knowledge is taken to be true, unless and until proven otherwise. This is the first standard of normality. Of course, background knowledge may be falsified by new experiences. If we are sure that some background theory is falsified, we give it up, even if we may go on (for lack of a better theory) to apply it in all cases in which it is not falsified.
Inductive reasoning leads to new knowledge by positing generalizations and theories that do not conflict with either empirical data or unchallenged background knowledge. Here the standard of normality is straightforward: a generalization (whether standing alone or derived from a theory) is true unless it conflicts with empirical data, with background knowledge, or with other generalizations.
The latter case deserves some clarification. Suppose that the empirical data contain the information that certain objects have property P, but that we do not know of any of these objects whether they have property Q. From these data follows by CL the disjunction of two negated generalizations:[4]
~(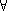 x)(Px
x)(Px Qx)
Qx) ~(
~(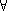 x)(Px
x)(Px ~Qx)
and hence one of both generalizations is bound to be false. As the data do not allow one to choose for any of the two generalizations, neither of them can be inductively derived.
~Qx)
and hence one of both generalizations is bound to be false. As the data do not allow one to choose for any of the two generalizations, neither of them can be inductively derived.
If one knows that some P are Q, ~(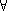 x)(Px
x)(Px ~Qx) is derivable from the premises. If no P is known to be ~Q, (
~Qx) is derivable from the premises. If no P is known to be ~Q, (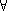 x)(Px
x)(Px Qx) is inductively derivable.[5] See the section on strategies on the connection between abnormalities.
Qx) is inductively derivable.[5] See the section on strategies on the connection between abnormalities.
-------
Notes (click on the number to return to the text)
|
[1]
|
Models are compared only with respect to the abnormalities they verify, not with respect to all formulas of the form (1) -- see the semantics. And in dynamic proofs only abnormalities, and no other formulas of the form (1), may occur in the fifth element of a line -- see the section on the dynamic proof theory.
|
|
[2]
|
Actually, the interpretation of a word heavily depends on the context. If two occurrences of the same word occur in a different context in the same text, we shall (unconsciously) interpret them differently. However, a word may have different meanings in the same text, even if the context does not reveal so.
|
|
[3]
|
Remark that several approaches are possible. One possibility is to count all abnormalities for some specific word (in the context of a language schema: one schematic letter). If two occurrences of a word have a different meaning, then it will still be supposed that all other occurrences have the same meaning as one of the first two occurrences with a different meaning. Such an adaptive logic will keep the meaning divergences minimal, and favour a situation in which divergent meanings occur only once. A different possibility is to conflate all abnormalities for the same word. How the meanings of the occurrences relate is then unimportant.
A different matter is that the approach might be refined by taking the linguistic context into account. The occurrence of a word in a specific expression or its occurrence in connection with other words might determine its meaning.
|
|
[4]
|
It is useful to specify that by a generalization is meant: the universal closure of a formula of the form (A B) where no quantifiers or individual constants occur in either A or B. B) where no quantifiers or individual constants occur in either A or B.
|
|
[5]
|
Together with the empirical data, derived generalizations lead to predictions (by CL).
Some adaptive logics of induction handle (at present simple) forms of prediction by analogy in a direct way. Thus if most but not all P are Q, these logics enable one to predict Qa from Pa – remark that (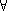 x)(Px x)(Px Qx) is not inductively derivable in this case. Qx) is not inductively derivable in this case.
|
Strategies
Consider again inductive reasoning. If ~(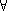 x)(Px
x)(Px Qx) is a consequence of the data, we say that (
Qx) is a consequence of the data, we say that (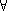 x)(Px
x)(Px Qx) behaves abnormally on the data. However, in the last example of the previous section,
Qx) behaves abnormally on the data. However, in the last example of the previous section,
~(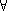 x)(Px
x)(Px Qx)
Qx) ~(
~(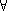 x)(Px
x)(Px ~Qx)
is a consequence of the data whereas neither disjunct is. This is typically a case of connected abnormalities: one of two or more formulas behaves abnormally on the premises, but the premises do not specify which one.
~Qx)
is a consequence of the data whereas neither disjunct is. This is typically a case of connected abnormalities: one of two or more formulas behaves abnormally on the premises, but the premises do not specify which one.
Let us consider another example of connected abnormalities, this time in an inconsistency-adaptive logic. Consider the premise set
{~p, ~q, p q, r
q, r ~s, p
~s, p s, q
s, q s}
If disjunction and conjunction behave as expected (that is, as in CL) in the lower limit logic, then
s}
If disjunction and conjunction behave as expected (that is, as in CL) in the lower limit logic, then
|
(1)
|
(p&~p) (q&~q) (q&~q)
|
is a consequence of the premises, whereas neither disjunct is. So, either p or q behaves abnormally on these premises, but the premises do not determine whether p or q behaves abnormally.
Remark that also
|
(2)
|
(p&~p) (q&~q) (q&~q) (r&~r) (r&~r)
|
is a consequence of this premise set (it follows from (1) by addition). This, however, does not make r in any way part of the connected abnormalities, precisely because the shorter disjunction of abnormalities (1) is derivable. In sum, the minimal disjunctions of abnormalities (that is, the shortest or strongest ones) determine which formulas are connected with respect to their abnormal behaviour on a given set of premises. Where Dab( ) abbreviates the disjunction of
) abbreviates the disjunction of 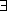 (A&~A) for all A in
(A&~A) for all A in  ,[1] Dab(
,[1] Dab( ) is called a Dab-formula. It is a minimal Dab-formula (a minimal disjunction of abnormalities) with respect to a set of premises
) is called a Dab-formula. It is a minimal Dab-formula (a minimal disjunction of abnormalities) with respect to a set of premises  iff there is no
iff there is no  '
'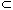
 such that Dab(
such that Dab( ') is a lower limit consequence of
') is a lower limit consequence of  .
.
With this in mind, it is easy to see the differences between different adaptive strategies.
The Simple strategy considers a formula A as abnormal iff A behaves abnormally on the premises. This strategy leads only to adequate results for very specific adaptive logics, viz. the ones in which all minimal Dab-formulas are singletons (sets that have one member). For such logics, the Reliability strategy (see below) and the Minimal Abnormality strategy (see below) reduce to the Simple strategy. There are such adaptive logics, for example the inconsistency-adaptive logics ANA from [Meh00b] and the ampliative adaptive logics of compatibility from [BM00a].
The Reliability strategy considers, for any Dab( ) that is a minimal Dab-formula with respect to a set of premises, all members of
) that is a minimal Dab-formula with respect to a set of premises, all members of  as unreliable. Thus, in view of (1), both p and q are unreliable with respect to the inconsistent premise set above. It follows that s is not an adaptive consequence of the inconsistent premise set on the Reliability strategy.
as unreliable. Thus, in view of (1), both p and q are unreliable with respect to the inconsistent premise set above. It follows that s is not an adaptive consequence of the inconsistent premise set on the Reliability strategy.
The Minimal Abnormality strategy delivers some more consequences than the Reliability strategy. This may easily be illustrated by the same inconsistent premise set. The Minimal Abnormality strategy interprets (1) as follows. Either p or q behaves abnormally. The premises do not determine which of both behaves abnormally, but we may suppose that, while the one behaves abnormally, the other behaves normally. This has a remarkable effect. If p behaves abnormally, q behaves normally and hence s is a consequence in view of ~q and q s. If q behaves abnormally, p behaves normally and hence s is a consequence in view of ~p and p
s. If q behaves abnormally, p behaves normally and hence s is a consequence in view of ~p and p s. Whichever is the case, s is an adaptive consequence of the inconsistent premise set.
s. Whichever is the case, s is an adaptive consequence of the inconsistent premise set.
The Reliability strategy is clear and simple with respect to the semantics and determines a simple and attractive dynamic proof theory. The minimal Abnormality strategy delivers (as remarked before) slightly more adaptive consequences than the Reliability strategy, it is extremely attractive from the semantic point of view, but it leads to a rather complicated proof theory.
These are the most important adaptive strategies. Some further strategies have been devised for characterizing consequence relations from the literature in terms of adaptive logics. These strategies are not very attractive for their own sake. They will be mentioned in subsequent sections, but will not be described here.
-------
Note (click on the number to return to the text)
|
[1]
|
As remarked in the section Characterization of an adaptive logic, it depends on the specific adaptive logic which formulas are abnormalities. For example, Dab( ) abbreviates a disjunction of negations of generalizations in the adaptive logic of induction that was discussed before. ) abbreviates a disjunction of negations of generalizations in the adaptive logic of induction that was discussed before.
|
Dynamic proof theory
The motor of the dynamics is the Derivability Adjustment Theorem. Let LLL be the lower limit logic and ULL be the upper limit logic, and let Dab( ) be a disjunction of (existentially quantified) abnormalities as before. For any adaptive logic, it should be proved that:
) be a disjunction of (existentially quantified) abnormalities as before. For any adaptive logic, it should be proved that:

 ULL A iff there is a
ULL A iff there is a  such that
such that 
 LLL A
LLL A Dab(
Dab( ) (Derivability Adjustment Theorem)
This leads to the interpretation: A is adaptively derivable from
) (Derivability Adjustment Theorem)
This leads to the interpretation: A is adaptively derivable from  iff the members of
iff the members of  behave normally on
behave normally on  .
.
As one cannot know in general (at the predicative level) whether the members of  behave normally on
behave normally on  , the proof theory is governed by two kinds of rules. The unconditional rules are those of the lower limit logic. A formula derived by one of them is as safe as the formulas to which the rule is applied. The rules validated by the upper limit logic but not by the lower limit logic are called conditional rules. If
, the proof theory is governed by two kinds of rules. The unconditional rules are those of the lower limit logic. A formula derived by one of them is as safe as the formulas to which the rule is applied. The rules validated by the upper limit logic but not by the lower limit logic are called conditional rules. If 
 LLL A
LLL A Dab(
Dab( ), then A may be derived from
), then A may be derived from  (a move justified by the ULL in view of the Derivability Adjustment Theorem) on the condition that the members of
(a move justified by the ULL in view of the Derivability Adjustment Theorem) on the condition that the members of  behave normally on
behave normally on  . Moreover, both kinds of rules carry over the conditions from the formulas to which they are applied.
. Moreover, both kinds of rules carry over the conditions from the formulas to which they are applied.
Apart from the premise rule, we need only two generic rules (rules in generic format). Their basic structure is as follows:[1]
|
PREM
|
Any premise may be added to the proof with Ø (the empty set) as its condition.
|
|
RU
|
If A1, ..., An  LLL B, then from A1, ..., An on the conditions LLL B, then from A1, ..., An on the conditions  1, ..., 1, ...,  n respectively, to derive B on the condition n respectively, to derive B on the condition  1 1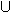 ... ...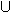  n. n.
|
|
RC
|
If A1, ..., An  LLL B LLL B Dab( Dab( ), then from A1, ..., An on the conditions ), then from A1, ..., An on the conditions  1, ..., 1, ...,  n respectively, to derive B on the condition n respectively, to derive B on the condition    1 1 ... ...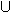  n. n.
|
For the sake of clarity, the lines of a dynamic proof consist of five elements: a line number, the formula derived, the line numbers of the formulas to which the rule is applied, the name of the rule, and the condition. Strictly speaking, the proof is formed by the second elements of the lines (just as in a usual proof). All other elements are part of the annotation.
We now come to the dynamics of the proofs. A formula, say, the second element of line i, is considered as derived iff the condition of line i fulfils certain criteria. If it does not fulfil those criteria, line i is marked. It is essential from a computational point of view that lines are not marked in view of criteria that refer to (the abstract notion of) derivability, but in view of criteria that depend only on the formulas that occur in the proof at a stage (which is a concrete matter). As the proof is extended from one stage to the next, the marks may change (be added or be removed). The underlying idea is that, as the proof is extended, more insight is gained in the premises. The marks depend on this insight.
The marks are governed by the Marking Definition,[2] which itself depends on the strategy. Most Marking Definitions depend on the minimal Dab-formulas that are derived at the stage of the proof with the empty set as their condition (which means that they are lower limit consequences of the premises). I only discuss the Marking Definition for the Reliability strategy.
Let  be the set of premises. The formulas that are unreliable with respect to
be the set of premises. The formulas that are unreliable with respect to  at stage s of the proof, Us(
at stage s of the proof, Us( ), are the elements of those
), are the elements of those  for which Dab(
for which Dab( ) is a minimal Dab-formula at stage s of the proof. The Marking Definition for the Reliability strategy reads:
) is a minimal Dab-formula at stage s of the proof. The Marking Definition for the Reliability strategy reads:
A line is marked at stage s of the proof iff some member of the condition of that line is a member of Us( ).
).
Here is a simple example of a dynamic proof. It is propositional, transparent, and there are no connected abnormalities. The lower limit logic is CLuN, which is full positive CL with A ~A as the only axiom on negation.[3] Remark that Modus Ponens is an unconditional rule (and hence resorts under the generic rule RU), whereas Modus Tollens and Disjunctive Syllogism are conditional rules (and hence resort under the generic rule RC).
~A as the only axiom on negation.[3] Remark that Modus Ponens is an unconditional rule (and hence resorts under the generic rule RU), whereas Modus Tollens and Disjunctive Syllogism are conditional rules (and hence resort under the generic rule RC).
| 1 | ~p&r | -- | PREM | Ø | |
| 2 | q p p | -- | PREM | Ø | |
| 3 | s ~r ~r | -- | PREM | Ø | |
| 4 | r p p | -- | PREM | Ø | |
| 5 | p ~r ~r | -- | PREM | Ø | |
| 6 | ~p | 1 | RU | Ø | |
| 7 | r | 1 | RU | Ø | |
| 8 | ~q | 2, 6 | RC | {p&~p} | marked at stage 10 |
| 9 | s | 3, 7 | RC | {r&~r} | marked at stage 10; unmarked at stage 11 |
| 10 | (p&~p) (r&~r) (r&~r) | 5, 6, 7 | RU | Ø | |
| 11 | p&~p | 4, 6, 7 | RU | Ø | |
This adaptive logic (known as ACLuN1) is decidable at the propositional level. The reader can easily check that line 8 will remain marked at all further stages of the proof. While r is unreliable at stage 10 of the proof, it is not unreliable at stage 11. For this reason, line 9 is unmarked at stage 11. It is easily seen that line 9 will remain unmarked at all later stages of the proof. Also, nothing much interesting is further derivable from these premises – just consequences by Addition, Irrelevance, Adjunction, and the like. The situation will be less transparent if the premises are more complex. For this reason we need some more theory.
At stage 9 of the proof above, ~q and s are derived from the premises. Neither of them is derived at stage 10 because the lines on which they occur are marked. However, s is derived at stage 11 (and at all later stages). The notion of derivability involved here is derivability at a stage. But clearly, we are more interested in a different sort of derivability, which I shall call final derivability. The underlying idea is clear enough: the formulas that occur on unmarked lines when the proof is completed. However, the proof cannot be completed (because the premises have infinitely many consequences). Still, we can define final derivability. Actually, its definition is the same for all adaptive logics known so far:
A is finally derived at line i of a proof at a stage iff line i is unmarked at that stage and, whenever line i is marked in an extension of the proof, then there is a further extension in which line i is not marked.
This definition is nice and simple; and (provided the rules and Marking Definition are correctly defined) final derivability is provably sound and complete with respect to the semantics (next section). However, the definition is not in itself very useful from a computational point of view (it does not enable one to decide which formulas are finally derivable from the premises). This has two effects. First, we need to formulate criteria that enable one to find out, in specific cases, that a formula has been finally derived. Next, when we are in undecidable waters, it needs to be shown that a proof at a stage provides one with a decent estimate of the finally derivable formulas, even if this estimate is always bound to be partly provisional.
-------
Notes (click on the number to return to the text)
|
[1]
|
This holds only for the simplest adaptive logics. For prioritized ones, for example, there may be conditional premise rules as well. Nevertheless, the basic idea and structure is always the same.
|
|
[2]
|
In some older papers, the marking definition is erroneously called a rule. The dynamics of the proofs is typically related to the fact that a line marked at a stage of the proof may be unmarked at the next stage, and vice versa (see the example of a proof in the text).
|
|
[3]
|
The propositional version is studied under the name PI in [Bat80]; the predicative version in [Bat99b].
|
Semantics
Adaptive logics have a so-called preferential semantics (the first one was presented in [Bat86a]). The plot is simple and straightforward. We start from the lower limit models of the set of premises  . From these, a selection is made in view of the abnormalities that are verified by the models. The specific selection is determined by the strategy.
. From these, a selection is made in view of the abnormalities that are verified by the models. The specific selection is determined by the strategy.
Consider again inconsistency-adaptive logics that have CLuN as their lower limit logic. The abnormalities are formulas of the form 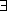 (A&~A), in which
(A&~A), in which 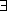 abbreviates an existential quantifier over any variable free in A as above. Let Ab(M) be the set of A for which the CLuN-model M verifies
abbreviates an existential quantifier over any variable free in A as above. Let Ab(M) be the set of A for which the CLuN-model M verifies 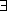 (A&~A).
(A&~A).
Let us first consider the Reliability strategy. We have seen in the section on Strategies that, for each set of premises  , there is a set of minimal Dab-consequences of
, there is a set of minimal Dab-consequences of  .[1] Let U(
.[1] Let U( ) contain the elements of those
) contain the elements of those  for which Dab(
for which Dab( ) is a minimal Dab-consequence of
) is a minimal Dab-consequence of  . A CLuN-model M of
. A CLuN-model M of  is a reliable model of
is a reliable model of  iff:
iff:
Ab(M) 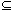 U(
U( )
in other words, if all abnormalities verified by M are unreliable with respect to
)
in other words, if all abnormalities verified by M are unreliable with respect to  . The adaptive (ACLuN1-)consequences of
. The adaptive (ACLuN1-)consequences of  are the formulas verified by all reliable models of
are the formulas verified by all reliable models of  .
.
Next, consider the Minimal Abnormality strategy (which leads to the inconsistency-adaptive logic ACLuN2). A CLuN-model M of  is a minimal abnormal model of
is a minimal abnormal model of  iff there is no CLuN-model M' of
iff there is no CLuN-model M' of  such that
such that
Ab(M') 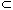 Ab(M)
in other words, iff no CLuN-model M' of
Ab(M)
in other words, iff no CLuN-model M' of  is (set theoretically) less abnormal than M. The adaptive (ACLuN2-)consequences of
is (set theoretically) less abnormal than M. The adaptive (ACLuN2-)consequences of  are the formulas verified by all minimal abnormal models of
are the formulas verified by all minimal abnormal models of  .[2]
.[2]
For all flat (that is: non-prioritized) adaptive logics, the preferences are purely logical in nature: they depend on the abnormalities verified by models of the premises.
It is instructive to consider the following schematic drawing:
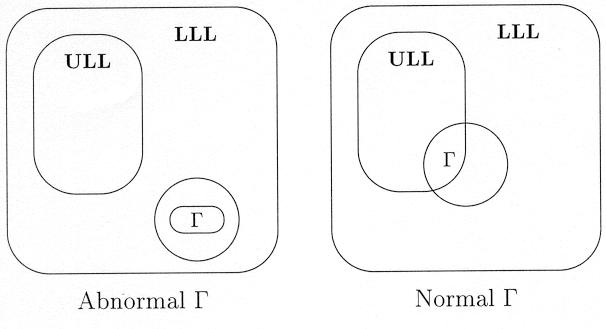
Remark that the ULL-models are a subset of the LLL-models. On both sides, the LLL-models of  are represented by the circle. If
are represented by the circle. If  has ULL-models (right side), its adaptive models coincide with its ULL-models. If
has ULL-models (right side), its adaptive models coincide with its ULL-models. If  has no ULL-models (left side), its adaptive models are still a subset of its LLL-models.
-------
has no ULL-models (left side), its adaptive models are still a subset of its LLL-models.
-------
Notes (click on the number to return to the text)
|
[1]
|
The minimal Dab-consequences of  are the shortest disjunctions of abnormalities that are derivable from are the shortest disjunctions of abnormalities that are derivable from  . This should not be confused with the minimal Dab-formulas derived from . This should not be confused with the minimal Dab-formulas derived from  at a stage of a proof (see Dynamic proof theory). at a stage of a proof (see Dynamic proof theory).
|
|
[2]
|
The Simple strategy selects those lower limit models M of  for which A is a member of Ab(M) iff for which A is a member of Ab(M) iff 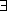 (A&~A) is a lower limit consequence of (A&~A) is a lower limit consequence of  . An adaptive logic defined by the Simple strategy is bound to assign the trivial consequence set to some . An adaptive logic defined by the Simple strategy is bound to assign the trivial consequence set to some  unless the lower limit logic warrants that all all minimal Dab-consequences of all unless the lower limit logic warrants that all all minimal Dab-consequences of all  count one disjunct only. count one disjunct only.
|
The block approach and dynamic semantics
Given the novel character of dynamic proofs, several problems had to be solved. I shall consider three such problems below. There solution (or at least a central step for it) derives from a same insight: the block approach. Moreover, this approach is useful in itself for our understanding of logic and meaning in general.
The first problem concerns the question whether the dynamics of the proofs is real. Remember that (in decently formulated adaptive logics) final derivability is sound and complete with respect to the semantic consequence relation. There is nothing dynamic about final derivability or semantic consequence. If they are our ultimate goal, is the dynamic character of the proof theory (and the instability of ‘derivability at a stage’) not either an illusion or the result of a clumsy formulation of the proof theory? For one thing, is there a semantic counterpart to the dynamics of the proofs?
The second problem is whether the notion of final derivability has any practical use? Any proof humans are able to write down will be a proof at a stage. As there is no positive test (see section The problem) for the consequence relation, it is always possible (in general) that an unmarked line (that has a non-empty fifth element) will be marked at a later stage. But certainly in some cases we should be able to find out that a line will not be marked at any later stage of the proof. In other words, we want to formulate criteria that, when they apply, warrant that a formula has been finally derived from a set of premises.
The third problem concerns the case in which no such criteria apply. If dynamic proofs are useful, then the formulas derived at a stage should, in one way or other, offer a sensible estimate of the formulas that are finally derivable from the premises. What might ‘sensible estimate’ mean here? For one thing, the estimate should become more reliable as the proof proceeds. Moreover, it should be possible to understand, from a metatheoretic point of view, why the estimate becomes more reliable.
So, let us turn to this block approach. As it is not typical for adaptive logics, I shall clarify it in terms of a proof in CL. Given an annotated proof, there are certain discriminations and identifications that the author of the proof has minimally made in order to construct the proof. For example, in order to apply Modus Ponens, one needs to see that one premise (the major one) consists of two formulas connected by an implication, that the other premise (the minor one) is identical to the antecedent of the major premise, whence one derives a formula that is identical to the consequent of the major premise. There is no need to know what the involved formulas are, as long as those discriminations and identifications are made. Let us call such unanalysed formulas ‘blocks’, and let us give each block a number, enabling us to make it clear that two blocks are identified. Here is an example of a simple CL-proof to which I shall apply the block analysis below.
|
1
|
(p q) q) (p&(~r (p&(~r ~p)) ~p))
|
Premise
|
|
2
|
p q q
|
Premise
|
|
3
|
p&(~r ~p) ~p)
|
1, 2; Modus Ponens
|
|
4
|
p
|
3; Simplification
|
|
5
|
p (p (p q) q)
|
4; Addition
|
Let us now, stage by stage, have a look at the block analysis of a proof (the minimal discriminations and identifications required to construct the proof). Writing down a premise does not require any discriminations or identifications. So, at stage 1, the block analysis reads:
|
1
|
[(p q) q) (p&(~r (p&(~r ~p))]1 ~p))]1
|
Premise
|
The block analysis of stage 2 is equally simple:
|
1
|
[(p q) q) (p&(~r (p&(~r ~p))]1 ~p))]1
|
Premise
|
|
2
|
[p q]2 q]2
|
Premise
|
Stage 3 requires that block 1 is analysed and that some blocks are identified:
|
1
|
[p q]2 q]2 [p&(~r [p&(~r ~p)]3 ~p)]3
|
Premise
|
|
2
|
[p q]2 q]2
|
Premise
|
|
3
|
[p&(~r ~p)]3 ~p)]3
|
1, 2; Modus Ponens
|
Similarly for stage 4:
|
1
|
[p q]2 q]2 ([p]4&[~r ([p]4&[~r ~p]5) ~p]5)
|
Premise
|
|
2
|
[p q]2 q]2
|
Premise
|
|
3
|
[p]4&[~r ~p]5 ~p]5
|
1, 2; Modus Ponens
|
|
4
|
[p]4
|
3; Simplification
|
Remark that block 2 was replaced by a block formula everywhere (if it were not, the proof would not be correct). Finally, here is stage 5:
|
1
|
[p q]2 q]2 ([p]4&[~r ([p]4&[~r ~p]5) ~p]5)
|
Premise
|
|
2
|
[p q]2 q]2
|
Premise
|
|
3
|
[p]4&[~r ~p]5 ~p]5
|
1, 2; Modus Ponens
|
|
4
|
[p]4
|
3; Simplification
|
|
5
|
[p]4 [p [p q]6 q]6
|
4; Addition
|
Remark that the content of block 6 is identical to that of block 2. However, in order to write the proof (up to stage 5), there is no need to identify both blocks. For this reason they are given a different number.
Suppose now that we consider the blocks as the elements of the language schema. The semantics for this language schema is structurally identical to the CL-semantics for the usual language schema: each different block is given a truth value, 0 or 1, and the values of compound formulas are derived from these in the usual way. Remark that there is no reason why v([p q]2) should be identical to v([p
q]2) should be identical to v([p q]6); these are different blocks and hence may receive different truth values.
q]6); these are different blocks and hence may receive different truth values.
Moving to the predicative level involves some complications, which will be skipped here. However, (as may be seen from [Bat95] or [Bat98a]) in that case too we obtain blocks that behave exactly like the elements of the usual predicative language schema.
The relation between different stages of a proof is semantically described by the consecutive block analyses. Thus, the transition from stage 2 to stage 3 in the above proof requires that v([p q]2
q]2 [p&(~r
[p&(~r ~p)]3) = v([(p
~p)]3) = v([(p q)
q) (p&(~r
(p&(~r ~p))]1) = 1. As v([p
~p))]1) = 1. As v([p q]2) = 1, it follows that v([p&(~r
q]2) = 1, it follows that v([p&(~r ~p)]3) = 1, as desired.
~p)]3) = 1, as desired.
The block analysis of dynamic proofs is very similar to that of CL-proofs. The basic difference is that Dab-formulas need to be transparent. This simply means that, if a Dab-formula is derived at some line, then the block analysis is pushed sufficiently far to reveal that it is a Dab-formula. Thus if, in an ACLuN1-proof, (p&~p) (q&~q) has been derived, then its block analysis will be ([p]10&~[p]10)
(q&~q) has been derived, then its block analysis will be ([p]10&~[p]10) ([q]15&~[q]15), in which the numbers of the blocks are obviously arbitrary.
([q]15&~[q]15), in which the numbers of the blocks are obviously arbitrary.
Consider the block analysis of a dynamic proof at a stage. It can be shown that, if a formula is derived at that stage, then the corresponding block formula is finally derived from the block premises (as determined by the stage). This provides us with a dynamic semantics, with respect to which derivability at a stage is provably sound and complete. This solves the first problem.
Some criteria for final derivability (second problem) are rather complicated, but the underlying idea is simple. Whether an abnormality, or a Dab-formula, that has not been derived at the present stage will be derivable at a later stage of the proof, depends on the question whether certain formulas occur within at present unanalysed blocks. In other words, we may obtain criteria by requiring that the block analysis is pushed sufficiently far to make sure that certain formulas occur transparently (that is: as separate blocks that all have the same number) within the block analysis of the proof at a stage.
The block analysis enables one to distinguish between informative and uninformative moves in a proof. The former restrict the models of the premises (as analysed at the present stage) whereas the latter do not. Thus, in the above proof, lines 1 to 4 are added by informative moves whereas line 5 is added by an uninformative move. As analysing moves restrict the models of the premises, these moves increase the information that the proof provides about the premises. This justifies the claim that formulas derived at a stage are finally derived in as far as one may tell in view of the information that the proof provides about the premises.
Remark that this information never decreases, even if it is not increased by uninformative moves. In other words, derivability at a stage provides an estimate of final derivability, the estimate becomes more reliable as the proof proceeds, and we understand why, from a metatheoretic point of view, the estimate becomes more reliable.[1]
The block approach has many other useful applications. Thus, by inducing a (set-theoretic) measure for the information provided by a proof about a set of premises, it enables one to solve the omniscience riddle. It offers interesting heuristic (or strategic) insights for proof search. It may be applied to analyse several forms of meaning change.[2]
-------
Notes (click on the number to return to the text)
|
[1]
|
As is usual for decisions based on fallible information, one has the choice between acting now or gathering more information. In the present case, the latter comes to continuing the proof (and the block analysis indicates the direction in view of what was said in the text about criteria). Which choice will be the justified one is obviously a pragmatic matter, largely determined by economic considerations.
|
|
[2]
|
More on all this is found in [Bat95]. An application to pragmatic aspects of the process of explanation is reported in [BM01a].
|
Some properties
It is useful to remark the following central difference between an inconsistency-adaptive logic and a usual paraconsistent logic. Where a monotonic paraconsistent logic invalidates certain rules of CL, an inconsistency-adaptive logics invalidates only certain applications of rules. As we have seen, most paraconsistent logics invalidate Disjunctive Syllogism. Inconsistency-adaptive logics invalidate only some of its applications. Which applications are invalidated depends on (the lower limit consequences of) the premises.
In general, corrective adaptive logics invalidate some applications of rules of the chosen standard of deduction, whereas ampliative adaptive logics validate some applications of rules that are not correct according to the chosen standard of deduction.
If a theorem is defined as a formula that is derivable from the empty set of premises, then the theorems of an adaptive logic coincide with the theorems of its upper limit logic. (The empty set of premises does indeed not involve any abnormalities.) If a theorem is defined as a formula that is derivable from all sets of premises, then the theorems of an adaptive logic coincide with the theorems of its lower limit logic. In this sense, adaptive logics have no specific theorems ‘of their own’.
It is often said that a semantics for a logic L defines a set of L-models, that the valid formulas are those verified by all L-models, and that the semantic consequences of  are those verified by all L-models of
are those verified by all L-models of  . If L is an adaptive logic, the first expression is confusing and the second is wrong. Adaptive logics have no models ‘of their own’. Let AL be an adaptive logic, LLL its lower limit logic, and ULL its upper limit logic. Each LLL-model is an AL-model of some
. If L is an adaptive logic, the first expression is confusing and the second is wrong. Adaptive logics have no models ‘of their own’. Let AL be an adaptive logic, LLL its lower limit logic, and ULL its upper limit logic. Each LLL-model is an AL-model of some  .[1] A formula is verified by all AL-models iff it is a theorem of ULL. A formula is verified by all AL-models of the empty set iff it is a theorem of LLL. The AL-semantic consequences of
.[1] A formula is verified by all AL-models iff it is a theorem of ULL. A formula is verified by all AL-models of the empty set iff it is a theorem of LLL. The AL-semantic consequences of  are indeed the formulas verified by all AL-models of
are indeed the formulas verified by all AL-models of  . However, the latter are not the AL-models that verify
. However, the latter are not the AL-models that verify  , but are a selection (determined by the strategy) of the LLL-models that verify
, but are a selection (determined by the strategy) of the LLL-models that verify  . (For example, the ACLuN1-models of
. (For example, the ACLuN1-models of  are the reliable CLuN-models of
are the reliable CLuN-models of  , as we have seen before.)
, as we have seen before.)
Strong reassurance: [Bat00a].
Tableau methods: [BM00b] and [BM01b].
An important recent result concerns adaptive logics in standard format. By relying only on properties of the standard format, it was proved for all these logics in [Bat07b], that their proof theory is sound and complete with respect to the semantics. In the same paper, many other properties of these adaptive logics were proven, including Reassurance, Strong Reassurance (Stopperedness, Smoothness), and Proof Invariance.
MORE SOON.
-------
Notes (click on the number to return to the text)
Flat and prioritized adaptive logics
A set of premises is called flat iff there is no priority ordering between them, otherwise it is called prioritized. So, let us call an adaptive logic flat iff it treats all premises on a par, and prioritized otherwise. The inconsistency-adaptive logics discussed before are all flat. They consider the case where (a theory or) set of premises is inconsistent, and where there is no reason to consider some of the premises as more reliable than the others. The matter is different for the adaptive logic of induction that was used as an example before. In the general case, the premises consist of empirical data as well as of background knowledge. But if the data contradict some background hypothesis, the straightforward and simple approach will give up that background generalization. This means that the underlying adaptive logic is prioritized: the data are given a higher priority than the background generalizations.
Most papers on adaptive logics, and especially the older ones, study flat adaptive logics. The basic problems lie there. These should be solved first. To extend the results to prioritized adaptive logics is a different (and usually less difficult) task.
Let us suppose that the premises are ordered in n different layers: < 1,
1,  2, ...,
2, ...,  n>, and that the members of any
n>, and that the members of any  i receive a higher priority than the members of
i receive a higher priority than the members of  i+1 (this is obviously a conventional matter). There are many ways to handle such prioritized sets of premises. One possibility is to introduce any premise with a subscript that indicates its priority. Anything derived from formulas that have the same subscript, will also receive this subscript; anything derived from formulas that have different subscripts will receive the highest of these subscripts. Remark that this also holds for Dab-formulas, which determine the formulas that are unreliable (at a stage of the proof). Sometimes a subscript referring to some priority level is attached to each member of the ‘condition’ of a formula; more often the subscript is attached to the set itself. For the Reliability strategy, lines are marked if some member of the condition is unreliable at its priority level.
i+1 (this is obviously a conventional matter). There are many ways to handle such prioritized sets of premises. One possibility is to introduce any premise with a subscript that indicates its priority. Anything derived from formulas that have the same subscript, will also receive this subscript; anything derived from formulas that have different subscripts will receive the highest of these subscripts. Remark that this also holds for Dab-formulas, which determine the formulas that are unreliable (at a stage of the proof). Sometimes a subscript referring to some priority level is attached to each member of the ‘condition’ of a formula; more often the subscript is attached to the set itself. For the Reliability strategy, lines are marked if some member of the condition is unreliable at its priority level.
Many prioritized adaptive logics have a conditional premise rule. This is because a premise of some priority level will itself be marked in view of formulas that have a higher priority. A typical example are the diagnosis logics from [BMPV03]. There, the premises of the highest priority are factual statements, and the premises of (an indefinite number of) lower priority levels are expectations. Expectations are introduced by a conditional premise rule, and have themselves (or rather, the singleton containing the expectation) as their condition. If an expectation is unreliable with respect to the factual statements,[1] all lines that have it in their condition -- this includes the premise line -- are marked. For most prioritized adaptive logics a derivable rule allows one to `downgrade' a derived formula to any lower priority. Thus from A4 one may derive A5 etc.
The basic idea that underlies the dynamic proof theory of prioritized adaptive logics is a very simple sophistication of the dynamic proof theory of the corresponding flat adaptive logic. Often the idea is as simple as the following. Suppose that A4 is derivable and that its condition is reliable at level 4. Suppose moreover that ~A5 is also derivable. For most prioritized adaptive logics, this entails that the condition of ~A5 is unreliable at level 5, and hence that ~A5 is marked whereas A4 is retained.
The semantics of prioritized adaptive logics is also a slight sophistication of the semantics of the corresponding flat adaptive logics. In the flat case, we start from the lower limit models of the premises and make a selection of them, in view of the abnormalities they verify, to obtain the adaptive models of the premises. In the prioritized case, one first makes this selection with respect to the abnormalities of the highest priority, next with respect to the abnormalities of the second highest priority, and so on.
When tackling a prioritized form of reasoning, the right policy seems to be to approach the problem in different steps. One first studies the flat adaptive logic required to handle the separate priority levels. Next one studies the sophistication required by combination of the different levels. Sometimes, it is helpful to consider a ‘prioritized knowledge base’ of the form < 1,
1,  2, ...,
2, ...,  n> as the sequence of unions <
n> as the sequence of unions < 1,
1,  1
1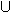
 2, ...,
2, ...,  1
1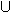 ...
...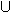
 n> and to look for a flat adaptive logic that derives the consequences that
n> and to look for a flat adaptive logic that derives the consequences that  1 should provide from
1 should provide from  1, derives the further consequences that
1, derives the further consequences that  2 should provide from
2 should provide from  1
1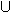
 2, etc.
2, etc.
-------
Notes (click on the number to return to the text)
|
[1]
|
In these logics, abnormalities are negations of expectations that are derivable from the data together with expectations of a higher priority. This is a typical case where the set of possible abnormalities is not determined by some logical form, but is, for each priority level except for the first one, identical to the premises at level.
|
Inconsistency-adaptive logics
The first inconsistency-adaptive logics [Back]
The proof theory of the first inconsistency-adaptive logic was studied in [Bat89a]; this system, then called DDL, is restricted to the propositional fragment and uses the Reliability strategy. The approach was also presented, especially with respect to discovery contexts, in [Bat85a].
The first semantics for the Minimal Abnormality strategy was presented in [Bat86a]. It was restricted to the propositional case.
Both logics were studied at the predicative level in [Bat99b]. This paper contains the proof theory as well as the semantics, and the central metatheoretic stuff. All aforementioned logics have the paraconsistent logic CLuN (or its propositional fragment) as their lower limit logic.
Inconsistency-adaptive logics that have CLuN as their lower limit logic have certain advantages in specific application contexts (especially cases where empirical theories were intended as consistent but turn out to be inconsistent). This was already defended in [Bat89a]. Quite different arguments are presented in [Bat03a] and [Bat02a].
Other inconsistency-adaptive logics [Back]
A different generalization of the Minimal Abnormality strategy to the predicative level was presented in [Pri91]; this logic has Priest's LP as its lower limit logic (but this is independent of the variant of the strategy). See [Bat99c] for a discussion of the variant of the strategy.
Especially for applications to mathematical contexts, the lower limit logic CLuNs -- see [BDC04], and [Bat80] for the propositional fragment (there called PIs). The adaptive logics obtained from CLuNs by the Reliability and Minimal Abnormality strategies have been characterized in passing, for example in [Bat00a], but deserve further systematic study.
In [Meh06a], an inconsistency-adaptive logic is presented that has Jaskowski's D2 as its lower limit logic. It is argued that the adaptive logic serves Jaskowski's aim better than D2.
A remarkable inconsistency-adaptive logic is presented in [Meh00b]. The lower limit logic, AN, validates disjunctive syllogism and all other analysing inferences (specified in the paper). The price to be paid is that Addition, Irrelevance, and similar non-analysing inferences are invalid in AN. It is argued that this logic offers a realistic tool for explicating a scientist's reasoning in an inconsistent context. The matter is also discussed in [Bat00b].
An adaptive logic for pragmatic truth (from [MdCC86]) is presented in [Meh02a].
Note on strong negation, bottom, and company [Back]
COMING SOON.
The standard application recipe [Back]
COMING SOON.
Other corrective adaptive logics
More gluts and gaps [Back]
Inconsistency-adaptive logics tolerate (but minimize) negation gluts. The idea to formulate logics that are adaptive with respect to negation gaps and with respect to gluts and gaps in other logics constants was presented and defended in [Bat97]. The technical problems to realize this were solved in [Bat99e] and [Bat01c]. These papers also discuss combinations of several gluts and gaps.
Ambiguity-adaptive logics [Back]
[Van97], [Van99] (see also [Bat02c] and [Batar] for a general formulation of the lower limit logic and its expressive power).
Adaptive logics with zero logic as lower limit [Back]
[Bat99e] and [Bat01c] also discuss the combination of gluts and gaps with respect to all logical constants and with respect to ambiguities in the non-logical constants. The lower limit logic does not validate any inference (not even A  A). Nevertheless, the adaptive logics interprets the premises as normally as possible, and delivers all CL-consequences if the premises have CL-models (that is: are normal with respect to CL).
A). Nevertheless, the adaptive logics interprets the premises as normally as possible, and delivers all CL-consequences if the premises have CL-models (that is: are normal with respect to CL).
Ampliative adaptive logics
COMING SOON.
-------
Notes (click on the number to return to the text)
Characterization of consequence relations described in the literature
It is the aim of the adaptive logic program to characterize all defeasible reasoning forms in terms of an adaptive logic in standard format. This was realized for a variety of defeasible reasoning forms, mostly by tackling such reasoning forms from scratch. Many defeasible reasoning forms have been decently described independently of the adaptive logic program. Quite a few of these were characterized by an adaptive logic in in standard format: [Bat00d], [Bat03b], [BV02] and [Ver03b]
for handling inconsistent knowledge bases as in [RM70]
, [BDP97]
, and [BDP99]
; [BMPar]
for the signed consequence relations from [BS98];
[DC00] and [Bat94] for default reasoning and circumscription,
documented in [Ant96], [Bre91], and [{\L}uk90]
(these are older results, not in standard format, that soon will be improved upon);
[Str] for rational closure from [LM92];
[SS] for abstract argumentation from [Dun95];
[PM08] for the belief merging protocols from [KPP02].
Several consequence relations have been characterized in terms of adaptive logics, sometimes under a translation. For some of them, strengthenings and other variants were developed.
[Bat94], [Bat00d], [Bat03b], [BV02], [BMPar], [DC00], [Van00b], [Van00a],
MORE SOON.
Applications
Argumentation [Back]
The central idea concerning the link between adaptive logics and argumentation is presented in [Bat96]. A central formal result in this respect is [Bat99e].
Induction [Back]
A first system may be found in [Bat05a]; given a set of data and (defeasible) background generalizations, generalizations as well as predictions are derived. Forthcoming work by Lieven Haesaert and Diderik Batens (falsified but provisionally retained background generalizations, inconsistent background theories).
Abduction [Back]
[Meh05]
[MVVDP02]
[MB06]
Explanation [Back]
A general argument was presented in [WDC02]. In [Bat05c], Hintikka's theory of the process of explanation (e.g., [HH05]) is generalized to include consistent as well as inconsistent situations. [BM01a] contains an adaptive logic for explanation seeking deduction as well as a logic of questions that enables one to generate derived questions in view of the verification of some possible initial condition. See also Abduction. Covering law explanations are considered in [WVD01].
Diagnosis [Back]
[WP99]
[PW02]
[BMPV03]
Scientific problem solving in an inconsistent context [Back]
[Meh93] [Meh02c] [Meh99a] [Meh02b] [Bat85b]
Scientific discovery and creativity [Back]
[Meh99b]
[Meh99c]
[Meh00a]
[Meh99d]
[MB96]
[Bat99a]
Discussions [Back]
[Ver03a]
[Batntb]
[Bat03b]
Other applications [Back]
Worldviews: [Bat99d]; characterization of the pure logic of relevant implication [Bat01a]; metaphors: [D’H02]; relations with dialectics: [Bat89a], [Bat89b]; recapturing classical reasoning from a dialetheist viewpoint: [Pri91]; general epistemology: [Bat04c].
MORE SOON.
Some historical remarks
COMING SOON.
-------
Notes (click on the number to return to the text)
[Top]
 is non-monotonic iff (if and only if) there is a formula A and there are sets of formulas
is non-monotonic iff (if and only if) there is a formula A and there are sets of formulas  and
and  ', such that
', such that 
 A whereas
A whereas 
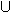
 '
' 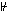 A (A is a consequence of
A (A is a consequence of  , but not of
, but not of  together with
together with  ').
').
 ) = {A |
) = {A | 
 L A} (the set of all formulas derivable from
L A} (the set of all formulas derivable from  by L).
by L).
 L, there are monotonic consequence relations
L, there are monotonic consequence relations  L1 and
L1 and  L2 such that
L2 such that 
 L A iff
L A iff 
 L1 B and
L1 B and 
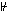 L2 C, in which there are certain relations between
L2 C, in which there are certain relations between  ,
,  and
and  on the one hand (these sets may all be identical) and between A, B and C on the other hand (A and B may be identical and C may be ~A), and in which
on the one hand (these sets may all be identical) and between A, B and C on the other hand (A and B may be identical and C may be ~A), and in which  L1 and
L1 and  L2 may be identical. If the latter two are undecidable, then even if there is a positive test for them and even if the relations between the sets and formulas are decidable, there is no positive test for
L2 may be identical. If the latter two are undecidable, then even if there is a positive test for them and even if the relations between the sets and formulas are decidable, there is no positive test for  L.
L.
 CnL(
CnL( x)(Px
x)(Px Qx)). In some (prioritized) adaptive logics, abnormalities (of some priority level) are negations of premises (of that priority) -- see the section on Flat and prioritized adaptive logics for an example.[1]
Qx)). In some (prioritized) adaptive logics, abnormalities (of some priority level) are negations of premises (of that priority) -- see the section on Flat and prioritized adaptive logics for an example.[1] B, ~A
B, ~A  (A&~A)
(A&~A)
 p2) expresses an abnormality of the sentential letter p, ~a4=a17 an abnormality for the individual constant a, etc. Remark that, on this approach, any schematic letter (but no other formula) may behave abnormally.
p2) expresses an abnormality of the sentential letter p, ~a4=a17 an abnormality for the individual constant a, etc. Remark that, on this approach, any schematic letter (but no other formula) may behave abnormally.