Sources in the history of algebra: arithmetical and recreational problems

Conspectus of problems from: Trattato di praticha d’arismetricha.
Transcription by: Pieraccini, Licia (1983) M° Biagio, Chasi exenplari alla regola dell'algibra. Nella trascelta a cura di Maestro Benedetto. Dal Codice L. VI. 21 della Biblioteca Comunale di Siena, Servizio Editoriale dell’Università, Siena.

BTP001 Truova uno numero che il terzo e il quarto di quel numero sia radice del detto numero. (p. 388v)
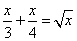
BTP002 Truova una quantità che tractone il 1/3 e il 1/4, el rimanente sia radi­ci di quel numero. (p. 388v)
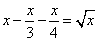
BTP003 Truova uno numero che trattone il 1/3 e il 1/4 e 4 più, jl rimanente sia la radice del numero. (p. 388v)
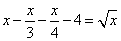
BTP004 Truova una quantità che moltiplichato il 1/3 chontro al ¼ faccino la detta quantità. (p. 388v)
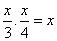
BTP005 Truova una quantità che moltiplichatone il 1/3 e 3 più per lo 1/4 e 4 più, quella moltiplichatione faccia la detta quantità. (p. 388v)
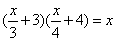
BTP006 Truova uno numero che trattone il 1/3 e del rimanente pre­so la radice, sia quanto e 3/4 del detto numero. (p. 389r)
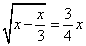
BTP007 Truova una quantità che aguntovj il 1/3 e il ¼ e la somma moltiplichata in se medesimo, faccia 20 chotanti che quel numero. (p. 389r)
BTP008 Truova una quantità che postovj su il 1/3 e il ¼ e 4 più e quella somma moltiplichata in se medesima, faccia 30 chotanti che’l detto numero. (p. 389r)
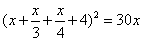
BTP009 Truova una quantità che postovi il 1/3 e il ¼ e 4 più, e nello che fanno moltiplichato per la metà del numero, faccia 40. (p. 389r)
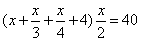
BTP010 Truova una quantità che moltiplichata glj 3/4 per gli 4/5, facci la radice di 20. (p. 389r)
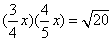
BTP011 Truova 2 quantità che tal parte sia l’una dell’altra chome 4 di 5 e moltiplichata l’una per l’altra faccino 100. (p. 389r)
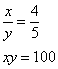
BTP012 Truova 2 quantità che tal parte sia l’una dell’altra chome 4 di 5, e moltiplichato chiaschuna quantità in sè e quelle moltiplichationj agunte insieme, faccino 100. (p. 389v)
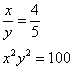
BTP013 Truova 2 numeri che tal parte sia l’uno dell’altro chome 4 di 5, e moltiplichato l’uno chontro all’altro faccino quanto agunti e numeri insieme. (p. 389v)
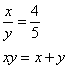
BTP014 Truova 2 numeri che tal parte sia l’uno dell’altro chome 4 di 5 e moltiplichato ciaschuno numero per se medesimo e agunte insieme le dette moltiplichationj, faccino quanto la guntione de’detti numerj. (p. 389v)
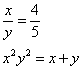
BTP015 Truova due quantità che tal parte sia l’una dell’altra chome 2 di 3, e moltiplichata l’una chontro all’altra faccino 6 chotanti che numerj, cioè le quantità, agunti insieme. (p. 389v)
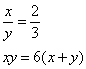
BTP016 Truova due quantità che tal parte sia l’una dell’altra chome 2 di 3. E moltiplichato ciaschuna quantità in se medesimo e agunti insieme, faccino 7 chotanti e 4 più che lla aguntione delle dette quantità. Adimandasj qualj sono le dette quantità. (p. 389v)
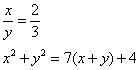
BTP017 Truova due numerj che ll’uno sia più che ll’altro 2. E partito lo maggiore per lo minore, ne vengha 7. (p. 390r)
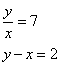
BTP018 Truova 2 quantità che lla maggiore sia 2 più che lla mi­nore, e moltiplichata l’una per l’altra, faccino 30. (p. 390r)
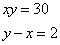
BTP019 Truova due numerj che 1l 'uno sia più che ll' altro 2. E moltiplichato ciaschuno per se medesimo e quelle molti­plichationj agunte insieme, faccino 30. (p. 390r)
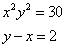
BTP020 Truova due numeri che ll’uno sia più che ll’altro 2. E moltiplichato ciaschuno per sè e tratta la moltiplicha­tione della minor quantità dalla moltiplichatione della maggiore, rimangha 30. (p. 390r)
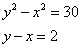
BTP021 Truova due numeri che 2/3 del primo sia quanto e 3/4 del sechondo, e moltiplichato l’uno chontro all’altro, faccia 32. (p. 390r)
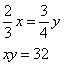
BTP022 Truova 2 quantità che ll’una sia più che ll’altra 2. E moltiplichata ciaschuna per sè, exenplo questa è scritta. Truova 2 quantità che glj 2/3 dell’una sieno quanto e ¾ dell’altra, e moltiplichata ciaschuna per se medesimo e quelle moltiplichationj agunti insieme faccino 30 più che’ numerj agunti agunti insieme. Adimandasj quanto è ciaschuna quantità. (p. 390v)
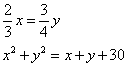
BTP023 Truova 3 quantità che tal parte sia la prima della se­chonda chome 3 di 4, e lla sechonda della terza chome 4 di 5. E moltiplichata la prima per la sechonda e quel­la moltiplichatione chontro alla terza, faccia quanto la guntione delle 3 quantità insieme. (p. 390v)
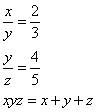
BTP024 Truova 3 quantità che tal parte sia la prima della sechonda chome 2 di 3 e tal parte sia la sechonda della terza chome 2 di 5. E moltiplichata la prima per la se­chonda e quel che fanno moltiplichato per la terza quan­tità, faccino 100. Adomandasj quanto sia ciaschuna quantità. (p. 390v)
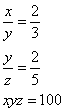
BTP025 Truova 3 quantità che glj 2/3 della prima sieno quanto e ¾ della sechonda, e gli 4/5 della sechonda sieno quanto glj 5/9 della terza. E moltiplichata la prima per la se­chonda e sopra la moltiplichatione agunta la terza quantità, faccia 10 chotanti che lla guntione de’detti numeri insieme. Adimandasj quanto fu ciaschuna quantità. (p. 391r)
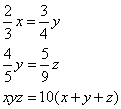
BTP026 Truova 4 quantità che lla prima sia alchuna chosa e la sechonda sia 2 più che lla prima, e la terza sia 1 più che lla sechonda e lla quarta sia 3 più che lla terza. E mol­tiplichata a prima per la quarta faccia quanto molti­plichata la sechonda nella terza. Adimandasj quanto so­no le dette quantità. (p. 391r)
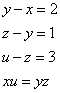
BTP027 Truova 2 quantità che glj ¾ della prima sieno quanto e 4/5 della sechonda e moltiplichato l’una per l’altra faccino la radice di 20. Adimandasj quali sono quelle quan­tità. (p. 391r)
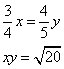
BTP028 Truova uno numero, overo una quantità, che moltiplicha­to il 1/3 più 1 della quantità per lo 1/4 più 1 della mede­sima quantità, faccino 20. (p. 391v)
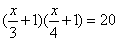
BTP029 Truova una quantità alla quale agunta la radice di 10 moltiplichata la somma per la detta quantità, faccia 9 chotanti che lla detta quantità. Adimandasj quale è detta quantità. (p. 391v)
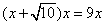
BTP030 Truova 2 numerj, overo 2 quantità, che moltiplichata la prima in sè faccia 3 chotanti della sechonda e moltipli­chata la sechonda in sè faccia 6 chotanti che lla pri­ma. Adimandasj qualj sono quelle quantità. (p. 391v)
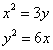
BTP031 Truova uno numero che moltiplichato in se medesimo e so­pra quello che fa agunto la radice, faccia 18. (p. 391v)
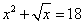
BTP032 Truova 2 quantità che l’una sia radice dell’altra, e moltiplichata ciaschuna quantità in sè e quelle molti­plichationj agunte insieme, faccino 100. (p. 392r)
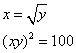
BTP033 Truova due numerj che ll’uno sia radice dell’altro, cioè 2 quantità. E moltiplichata l’una chontro all’altra, facciono 100. (p. 392r)
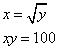
BTP034 Truova 4 numerj che’ sechondo sia 2 chotanti che’ pri­mo, e il terzo sia 2 chotanti del sechondo, e il quarto sia 2 chotanti che’ terzo, e lo terzo sia la radice di tutti e 4 e detti numerj meno uno, cioè sia uno meno che lla radice di tutti e 4. (p. 392r)
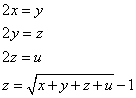
BTP035 Truova 3 quantità che lla prima sia il ¼ e il 1/9 ciò che sono gli altrj 2, e il sechondo sia più uno che ll radice di tutti e 3, e il terzo numero sia il terzo e il ¼ del sechondo e di se medesimo e più 7. Adimanda­sj quanto fu ciaschuna quantità. (p. 392r)
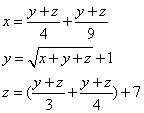
BTP036 Truova una quantità che lla sua radice sia 5 meno che la detta quantità. (p. 392v)
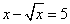
BTP037 Truova 2 quantità che gli 3/4 della sechonda meno 8, sieno quanto la prima. E partito quello della sechonda per la prima, ne vengha 8. (p. 392v)
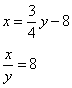
BTP038 Fa’ di 10 2 parti, che moltiplichata ciaschuna parte per se medesima e quelle 2 moltiplichationj agunte insieme, faccino 90. Adimandasj qualj sono le dette parti. (p. 392v)
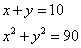
BTP039 Fa’ di 10 2 parti che moltiplichata l’una per l’altra, faccia 18. (p. 393r)
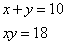
BTP040 Fa’ di 10 2 parti, che moltiplichata ciaschuna per sè e tratta l’una dell’altra, rimangha 20. (p. 393r)
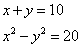
BTP041 Fa’ di 10 2 parti che ll’una sia 5 più che lla radice l’altra. (p. 393r)
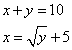
BTP042 Fa’ di 10 due parti che’l terzo dell’una sia quanto la radice dell’altra. (p. 393v)
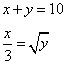
BTP043 Fa’ di 10 due parti che lla radice della maggiore parte sia uno più che lla radice della minore parte. (p. 393v)
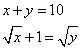
BTP044 Fa’ di 10 2 parti che’ quadrati d'amendunj le parti a­gunti insieme faccino 3 chotanti che moltiplichata l’una parte chontro all’altra. (p. 393v)
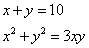
BTP045 Fa’ di dieci due parti la lla maggiore sia più che lla minore quanto è la radice della minore. (p. 393v-394r)
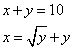
BTP046 Fa’ di 10 3 parti che partita la prima per la terza ne vengha 20 più che lla radice della sechonda. Adimandasj qualj sieno le dette parti. (p. 394r)
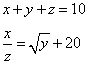
BTP047 Fa’ di 10 3 parti che lla prima sia 2 chotanti e uno più che lla sechonda e la terza sia sia la radice del­l’altre 2 parti. (p. 394r)
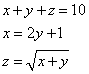
BTP048 Fa’ di 10 3 parti che loro quadrati sieno 54. Adimandasj qualj sieno queste partj. (p. 394r)
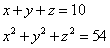
BTP049 Fa’ di 10 2 parti che moltiplichata l’una chontro all’altra e quel che fa partito nella differentia che è dalla una parte all’altra, ne vengha 10. (p. 394v)
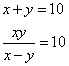
BTP050 Fa’ di 10 2 parti che moltiplichata l’una per l’altra faccia la differentia che è dall’una all’altra. (p. 394v)
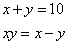
BTP051 Fa’ di 10 2 parti che moltiplichata l’una parte chontro all’altra e quel che fa diviso nella differentia che è dall’una all’altra, ne vengha 7 più che lla detta diffe­rentia. Adimandasj qualj sono le dette parti. (p. 394v)
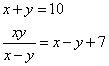
BTP052 Fa’ di 10 2 parti che preso la radice di ciaschuna parte e agunte insieme faccino 4. (p. 395r)
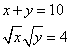
BTP053 Fa’ di 10 2 parti che moltiplichata la minore parte per la differentia che è dall’una parte all’altra, faccia la maggiore parte. Adimandasj qualj sono quelle parti. (p. 395r)
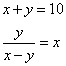
BTP054 Fa’ di 10 due parti che moltiplichata l’una parta chontro all’altra faccia quanto moltiplichata per se medesi­mo la differentia che è da ciaschuna parte. (p. 395r)
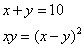
BTP055 Fa’ di 10 2 parti che moltiplichato la radice dell’una per la radice dell’altra, faccino la differentia che è dall’una all’altra. (p. 395v)
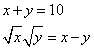
BTP056 Fa’ di 10 2 parti che moltiplichata la prima per radice di 18 faccia 3 chotanti della sechonda parte. (p. 395v)
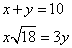
BTP057 Truova una quantità che moltiplichato quel che rimane a trarne il 1/5 e il 1/6 in se medesimo, faccia 100. Adiman­dasj quale è quella quantità. (p. 396r)
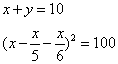
BTP058 Uno fa 2 viaggi, al primo viaggio radoppia e suoi d. e spende 6 f., al sechondo si trovò moltiplichati i suoj d. per se medisimo e spese 16 f., e infine de detti viaggi e’ si trovò 1000 f. Adimandasj chon quanti si mosse. (p. 396r)
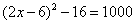
BTP059 Egli è un tondo che tutto è quadrato 1000 braccia. Adimandasj quanto è il suo diametro. (p. 396r)
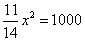
BTP060 Truova uno numero che moltiplichato in se e quello che fanno moltiplichato nella radice di 7, faccia 40. (p. 396r)
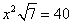
BTP061 Truova 3 quantità che tal parte sia la prima della se­chonda chome 4 di 5, e lla sechonda della terza chome 5 di 8. E moltiplichata la prima per la sechonda faccia la terza quantità. (p. 396r)
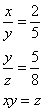
BTP062 Truova uno numero che postovj su la sua radice, faccia 3 chotanti che’l numero. (p. 396v)
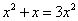
BTP063 Uno merchatante chomperò 3 anella d’oro, le qualj fra tutte e 3 chostarono 200 f. E’l primo chostò una quanti­tà di d., jl sechondo chostò 2 chotanti chotanti che’l primo e più 2 f., e il terzo chostò quel che fa moltiplichato il chosto del primo nel chosto del sechondo meno 9 f. Adimandasj quello che chostò ciaschuno per sè. (p. 396v)
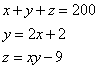
BTP064 Uno chomperò la channa del panno alquanti f. E poj, spese 60 f. in panno alla medesima ragione. E poj agunse insieme le braccia del panno ch’eglj aveva chomperato e i f. ch’eglj aveva speso e la somma fe’ 117. Adimanda­sj quello che chostò la channa del panno e quanto panno cho però. (p. 396v)
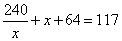
BTP065 Uno fa 2 viaggi. Al primo viaggio guadagnia 6, al se­chondo viaggio guadagnia alla medesima ragione. E dipoj si trovò 27. Adimandasj chon quanti si mosse. (p. 397r)
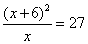
BTP066 Uno fa alquanti viaggi e tanti viaggi quant’eglj fa tan­ti d. porta. E a ognj viaggio guadagnia 25 per 100. E quando à chonpiuto e viaggi ed e’si truova 40 per 100. Adimandasj quanti d. porta e quantj viaggi fece. (p. 397r)
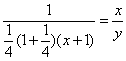
BTP067 Truova 2 numerj che tal parte sia l’uno dell’altro chome 5 di 7. E moltiplichato l’uno chontro all’altro, faccia 30 più che agunti e numerj insieme. Adimandasj qualj so­no e numerj, overo quello 2 quantità. (p. 397v)
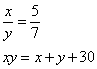
BTP068 Truova 2 quantità che moltiplichata la prima in se medesima faccia 27 chotanti dell’altra e moltiplichato la sechonta quantità per la prima fanno 1000. Adimandasj qualj furono le dette quantità. (p. 397v)
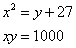
BTP069 Truova 3 quantità che tal parte sia la prima della se­chonda chome 2 di 3 e tal parte sia la sechonda della terza chome 3 di 4. E moltiplichato il primo nel sechon­do, e quel che fa nel terzo, faccia 1000. Andimandasj quali sono quelle quantità. (p. 397v-398r)
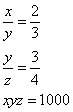
BTP069b Uno prestò a un altro 100 l. per 3 annj e nella fine de’ 3 annj riebbe tra merito e chapitale 172 l. 16s. Adimandasj a quanto stettono i suoj d. per centinaio l’anno a fface chapo d’anno. (p. 298r)
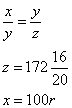
BTP070 Truovamj 3 numerj che tal parte sia il primo del sechon­do chome 3 di 5, e tal parte sia il sechondo del terzo chome 5 di 7, e moltiplichato il primo nel sechondo, e quel che fa nel terzo, faccia 9 chotanti che aguntj e detti numerj insieme. (p. 398r)
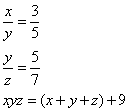
BTP071 Truova 3 numerj che tal parte sia il primo del sechondo chome 3 di 7, e tal parte sia il sechondo del terzo cho­me 7 di 11. E moltiplichato il primo per lo sechondo e quel che fa per lo terzo, faccia 7 chotanti che’l qua­drato della somma di tutti e numeri. Adimandasj quanto fu ciaschuno numero. (p. 398v)
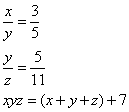
BTP072 Truova due numeri che moltiplichato il primo in se mede­imo faccino 4 chotanti dello sechondo, e moltiplichato il sechondo numero per lo primo numero fanno 7 chotanti che moltiplichato il primo numero in se medesimo. Adi­nandasj quali sono quei numerj. (p. 398v)
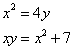
BTP073 Truova 3 numeri che tal parte sia il primo del sechondo chome 2 di 3, e tal parte sia il sechondo del terzo cho­me 3 di 4, e moltiplichato el primo per lo sechondo e quel che fa per lo terzo e a questa quantità agunta la moltiplichatione della guntione di ciaschuno del numeri moltiplichato in sè, faccino 78 2/3 volte che lo quadrato de’ numerj agunta insieme. (p. 398v)
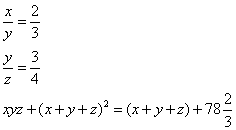
BTP074 Truova 3 quantità che moltiplicatha la prima in se mede­simo faccia 2 chotanti che lla sechonda, e moltiplichato la sechonda quantità per la prima faccino 3 chotanti che lla terza quantità, e agunto la sechonda quantità cholla terza quantità faccino 7 chotanti che lla prima quanti­tà. Adimandasj quanto fa ciaschuna quantità. (p. 399r)
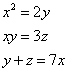
BTP075 Truova 3 numerj che tal parte sia il primo del sechondo chome 3 di 4, e moltiplichato il primo nel sechondo e quel che fa nel terzo e a questa moltiplichatione agunto 16 volte quel che faranno tra tutti e 3 e numerj, quella somma sia 2 chotantj che’l quadrato della aguntione di tutti e 3 gli numerj. (p. 399r)
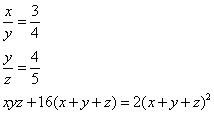
BTP076 Truovamj 3 numerj che tal parte sia l’uno dell’altro, cioè il primo del sechondo, chome 2 di 5, e il sechondo del terzo chome 5 di 8. E moltiplichato il primo per lo sechondo e quello che fa per lo terzo, faccia quanto il quadrato della aguntione di tuttj e numerj aguntovj 3 volte la somma di tutti e numerj. Adimandasj quanto fu ciaschuno numero. (p. 399v)
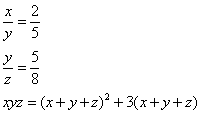
BTP077 Uno fa 2 viaggi: al primo radoppia e duoj d. e spende 8, al sechondo moltiplicha e d. ch’egli à in se medesimi e spende 12, e truovasj 244 d. Adimandasj chon quanti si mosse. (p. 399v)
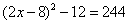
BTP078 Truova 2 quantità che moltiplichata la prima in se mede­sima faccia 2 chotantj che ll’altra e moltiplichata la sechonda in se medesimo faccia 1000. Adimandasj quanto fu ciaschuna quantità. (p. 399v)
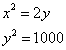
BTP079 Uno prestò a un altro 1000 l. per 4 annj a fare chapo d’anno. E quando e venne nella fine de’ 4 annj ad eglj gli rende tra di chapitale e merito 14641 1. Adimandasj a quanto stettono e suoj d. per 1000. (p. 400r)
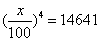
BTP080 Truova 4 numerj che tal parte sia il primo del sechondo chome 2 di 3, e tal parte sia il sechondo del terzo chome 3 di 5, e tal parte sia il terzo del quarto chome 5 i 10. E moltiplichato il primo nel sechondo e quel che a nel terzo e quello che fa nel quarto, faccia 405 cho­anti che numerj aguntj insieme. Adimandasj quanto era ciaschuno numero. (p. 400r)
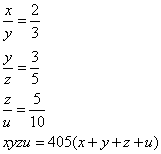
BTP081 Truova 2 numerj che moltiplichato il primo in se medesi­mo faccia 3 chotanti del sechondo e moltiplichato il se­chondo in se medesimo, faccia 24 chotanti che’l primo numero. Adimandasj quanto era ciaschuno numero. (p. 400r)
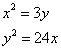
BTP082 Truova 4 quantità che tal parte sia la prima della sechonda chome 3 di 4, e lla sechonda della terza chome 4 di 5, e la terza della quarta chome 5 di 6. E molti­plichato el primo nel sechondo e ciò che fa per lo terzo e quello che fa moltiplichato nella quarta quantità, faccia 20 chotanti che’l quadrato della aguntione di tutti e numerj. Adimandasj qual sia ciaschuna delle det­te quantità. (p. 400r-400v)
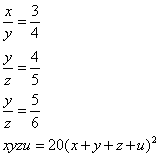
BTP083 Uno sta a uno fondacho 4 anni, nel quale tempo a’ di sa­laro 100 f. jn questo modo che’l primo anno à una quantità di d., el sechondo anno a più salaro, il terzo anno crescie il salare alla medesima ragione, e chosj il quarto anno crescie alla medesima ragione. E sappiamo che tra’l primo e il terzo anno eglj à 40 f., e tra’1 sechondo e 4° anno egli à 60 f.. Adimandasj quanto ebbe cia­chuno anno. (p. 400v)
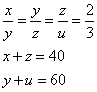
BTP084 Truova 3 quantità che moltiplichata la prima in se mede­simo faccia 2 chotanti che lla sechonda, e lla sechonda moltiplichata in se medesimo fa 3 chotanti della terza, e la terza quantità è 4 chotanti che lla moltiplichatio­ne della prima nella sechonda. Adimandasj quanto è cia­schuna quantità. (p. 400v)
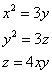
BTP085 Truova 3 quantità delle qualj la prima moltiplichata in sè medesima, faccia 3 chotanti della sechonda, e la sechonda quantità, moltiplichata in se medesima, faccia 2 chotanti della terza quantità, e agunto alla terza quantità la moltiplichatione della prima nella sechonda, fanno 24 chotanti della sechonda quantità. Adimandasj quanto è ciaschuna quantità. (p. 401r)
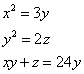
BTP086 Truova 3 quantità che tal parte sia la prima della se­chonda chome 2 di 3, e tal parte sia la sechonda della terza chome 3 di 4, e moltiplichata ciascuna quantità in se medesima e quelle moltiplichationj agunte insieme e quello moltiplichato in sè e sopra questa moltiplicha­tione agunto e quadrati de’ detti numerj faccia 100 cho­tanti che lla moltiplichatione della prima nella sechon­da e ciò che fa nella terza. Adimandasj quanto fu cia­schuna quantità. (p. 401r)
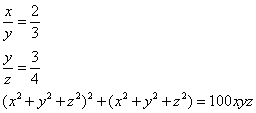
BTP087 Truova 4 quantità che tal parte sia la prima della se­chonda chome 2 di 3 e tal parte sia la sechonda della terza chome 3 di 4 e tal parte sua la terza della quarta chome 4 di 5. E moltiplichato la prima chontro alla se­chonda e quello che fa chontro alla terza e quello che fa chontro al quarto, faccia quanto moltiplichato cia­schuno numero in sè e lle moltiplichationj agunte insie­me più la moltiplichatione de’ detti numeri moltiplicha­ti nellj dettij quadrati, cioè nel quadrato di quei numeri. Adimandasj quanto fu ciaschuna quantità. (p. 401v)
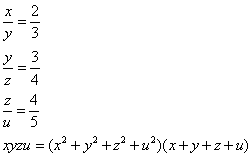
BTP088 Uno prestò a un altro 50 f. e 120 l . di picciolj. Quando viene in chapo dell’anno e quelli gli rende il suo chapitale, e per lo merito de’ 50 f. gli rende 5 f. e 7 l. di picciolj, e per lo merito di 120 l. di picciolj, gli ren­de 4 f. 5 l. di picciolj. Adimandasj quello valse el f. (p. 402r)
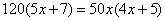
BTP089 Uno prestò a un altro 50 f e 150 l. di picciolj. Quando viene in chapo d’alchuno tempo e quelli gli rende il suo chapitale e per merito de’ 50 f. si gli rende 10 f. meno 5 l., e per merito delle 150 l. si diè 40 l. meno 5 f . Admindasj che calse il f. (p. 402r)
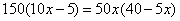
BTP090 Fa’ di 100 due parti che presa la radice di ciaschuna parte e agunte insieme faccino 14. (p. 402v)
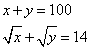
BTP091 Una choppa di 3 parti, cioè il ghambo, el choperchio, el nappo. El ghambo pesa il 1/3 e il 1/4 di ciò che pesa el coperchio el nappo, el choperchio pesa il 1/5 e il 1/6 di se medesimo, el nappo pesa tanto che moltiplichato per sè fa ciò che pesa tutta la choppa. Admimandasj che pesa tutta la choppa e quanto pesa ciaschuna parte. (p. 402v)
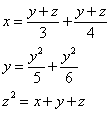
BTP092 Uno fa 3 viaggi, al sechondo viaggio guadagniò il 1/3 del suo chapitale più 2 e guadagniò alla medesima ragione che al primo viaggio. E chosj al terzo viaggio guadagniò a lla medesima ragione, e poi si trovò 16 2/3. Adimando chon quanti si mosse. (p. 402v-403r)
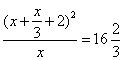
BTP093 Uno à 30 libre di muneta a una certa legha, e a’ 40 libre di muneta a un’altra legha, e a’ 50 libre di mune­ta a un’altra legha. Allo fonduto e’ trovollo sotto sopra a llegha di 7 once. Ed era la legha della libra del­le 30 libre alla libra delle 40 libre, chome la legha della libra delle 40 libre alla legha delle libre del 50 libre. Adimandasj di che legha era ciaschuna libra. (p. 403r)
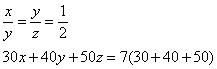
BTP094 Uno fa 2 viaggi: al primo viaggio guadagnia 8, al se­chondo perde a quella medesima ragione ch’egli à guada­gniato al primo, poi si truova 12 f. Adimandasj chon quanti d. si mosse. (p. 403r)
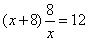
BTP095 Uno può avere d’uno suo f. alquanti aghontanj e vuole 2 chotanti meno 6 bologninj e chambiati 39 f. à avuto 360 aghontanj e 360 bologninj. Adimandasj che valse il f. (p. 403v)
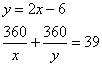
BTP096 Uno prestò a un altro 100 l. per 4 anni e vuole che suoi d. sieno meritati a 4 d. la l. al mese. E rivuole ognj anno una medesima quantità. Adimandasj che debba avere l'anno. (p. 403v)
BTP097 Uno prestò a un altro d. e non so quanti, e quando viene in chapo dell’anno e quelli gli rende tra merito e chapita­le 100 1. E quegli gli prestò un altro a quella medesi­ma ragione. E quando viene in chapo del sechondo anno ed egli gli rende tanti d. di merito che agunto al meri­to del primo anno fanno 45 1. Adimandasj quanti d. pre­stò prima. (p. 404r)
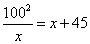
BTP098 Uno chomperò tra grano e orzo 10 staie, e spese nel gra­no 40 s. e nell’orzo 40 s., e chostoglj più lo staio del grano che llo staio dell’orzo 3 s. Adimandasj quello che chostò lo staio dell’orzo e che chostò lo staio del grano e quanto orzo e quanto grano chonperò. (p. 404r)
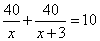
BTP099 Uno presta a un altro una quantità di d. e in chapo d’uno anno gli rende 60 f. Ed egli prestò 60 f. a un altro a uno d. a uno d. più per l. al mese che prima e in chapo del sechondo anno a choluj gli diè di merito tanto che il merito del primo anno fu al merito del sechondo chome 2 a 3. Adimandasj quanti d. gli pre­stò e a quanto per l. al mese è. (p. 404v)
BTP100 Uno prestò a un altro d. non so quanti nè a quanto per lira al mese, e quando viene in chapo dell'anno ed è dice tieni e tuoi d. che sono tra di chapitale e merito 100 1. E questo dice io non gli voglio, ma tieglj un altro anno a uno d. la l. al mese meno che non facessi anno. E in chapo del sechondo anno gli rende 25 1. meno che’l doppio del chapitale del primo anno. Adimandasj quanti furono e d. che gli prestò. (p. 404v)
BTP101 Uno à uno schachiere e chome noi sappiamo lo schachiere à in tutto 64 quadretti de’ quali n’è 28 intorno e 36 dentro e sappiamo che anoverando per ciaschuno lato sono 8 chotando amendunj e chanti, vorrebbe fare uno chachie­re che avessi altretantj quadratti nel mezo quanto in­torno intorno, vo’ sapere quanti quadrutti sarà per faccia ad anoverare per faccia ciaschuno chanto. (p. 405r)
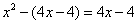
BTP102 Uno chonperò grano e orzo e spese 120 s. in orzo e 120 s. in grano, e chostoglj lo staio del grano 3 s. più che llo staio dell'orzo. E chonperò 2 staia più d’orzo che di grano. Adimandasj quanto valse lo staio dell’orzo e quanto lo staio del grano e quante staia d’orzo e quante staia di grano chonperò. (p. 405r)
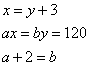
BTP103 Truova 2 numerj, overo 2 quantità, che sieno in propor­tione chome 5 a 7, cioè che lla prima quantità sia alla sechonda chome 5 a 7, e moltiplichate l’una per l’altra e aguntovj 9 faccino quanto moltiplichato la guntione delle dette quantità per 9. Adimandasj qualj sono le dette quantità. (p. 405v)
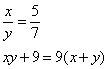
BTP104 Truova 3 quantità che lla prima sia il 1/3 e il 1/4 dell’al­tre 2, e lla sechonda sia uno più della radice di tutte e 3, e la terza sia il 1/4 e il 1/5 di sè [medisimo] e della sechonda. Adimandasj qualj sono queste quantità. (p. 405v)
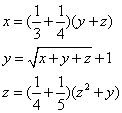
BTP105 Truova 3 numerj che moltiplichato lo primo per se mede­simo e llo sechondo per se medesimo e quelle moltiplichationj agunte insieme faccino quanto moltiplichare il terzo numero in sè, e moltiplichato il primo per lo terzo faccia quanto moltiplichare il sechondo in se me­desimo. Adimandasj qualj sono e detti numerj. (p. 405v-406r)
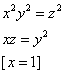
BTP106 Truova due numerj che l’uno sia la radice dell’altro e moltiplichato ciaschuno in se medesimo e agunte le moltiplichationj insieme faccino 20. (p. 406r)
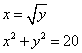
BTP107 Fa’ di 10 due parti che moltiplichato l’una per l’altra e diviso per la radice della loro differentia ne vengha la radice della detta differentia. Questa non è altri­menti proposto se non fa' di 10 due parti che moltipli­chata l’una per l’altra faccia la differentia che è dall’una all’altra. (p. 406r)
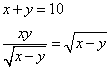
BTP108 Fa’ di 10 2 parti che moltiplichato l’una per l’altra faccino 4 chotanti che partita la maggiore per la mino­re. Adimandasj qualj fieno le dette parti. (p. 406r)
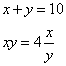
BTP109 Uno fa alquantj viaggi e tanti viaggi quant’eglj fa tan­ti d. porta. A ogni viaggio guadagnia a 40 per 100 e in chapo di tutti e viaggi si truova fatto d’ogni d. 6. Adimandasj chon quanti d. si mosse. (p. 406v)
BTP110 Uno fa alquanti viaggj e porta alquanti d. e fa 2 cho­tanti viaggi e 2 più, che non porta d. E a ognj viaggio guadagnia a 50 per 100. E quando à chonpiuti e suo’ viaggj, si truova d’ognj d. 30. Adumandasj chon quanti si mosse e quanti viaggi fece. (p. 407r)
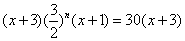
BTP111 Truova due numerj che i 3/4 dell’uno sia quanto gli 4/5 dell’altro, e moltiplichato ciaschuno numero in se me­desimo e le moltiplichationj agunte insieme faccino ra­ice di 20. Adimandasj quali sono e detti numerj. (p. 407v)
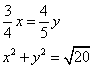
BTP112 Uno chonpera alquante huova alquanti d. e tante huova quant’eglj chonperò tanti d. gli diostò l’uovo. Poi chon­però uno huovo 6 d. e agunsolo agli altri e trovò che gli venisse la choppia sotto sopra 7 d. Adimandasj quante huova chonperò e quanti d. gli chostò l’uno. (p. 407v)
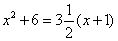
BTP113 Uno spese 6 d. in uova, e quante huova ebbe a d. tanti d. rivende l’uovo e trovossj guadagnato 2 d. per uovo. Adimandasj quante huova chonperò. (p. 407v)
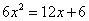