Diderik Batens en Joke Meheus
LOGICA II (tweede bachelor Wijsbegeerte)
Enkele nuttige oefeningen
Hoofdpagina [uw commentaar] [Terug]
Voorlopig is slechts beschikbaar wat volgt:
-
Toelichting
-
Documenten en ‘theoretische’ vragen
-
Taalschema’s
-
Semantische clausules voor enkele ongewone connectieven
-
Enkele oefeningen over de metatheorie van PC
-
Geldigheid in het propositioneel fragment van de paraconsistente logica CLuN
-
Geldigheid in het propositioneel fragment van de paravolledige logica CLaN
-
Tableaumethoden voor eenvoudige propositionele logica’s
-
Enkele vragen over modale logica’s
-
Het theorema van Gödel
Op wat onderlijnd is kan u klikken. Deze pagina wordt geregeld bijgewerkt — kijk af en toe eens opnieuw.
Toelichting
Deze oefeningen helpen u het vak goed te studeren, maar helpen u ook uw studiemethode bij te sturen. Wanneer u na het studeren van de stof niet weet hoe een oefening aan te pakken, ga dan na wat u bij het studeren hebt overzien en hoe u dat in het vervolg kunt vermijden.
Voorlopig werden vooral technische oefeningen opgenomen. Dat komt omdat daaraan meer behoefte bestaat dan aan meer filosofische vragen over de stof. Ook aan deze laatste wordt echter gewerkt.
Op het examen komen deze oefeningen in geen geval terug. Het heeft dan ook geen nut de oplossingen te kennen. Wat nut heeft is het zoeken naar de oplossingen. Daarom zullen de begeleiders u hierbij eventueel wel op weg helpen, maar zullen ze u de oplossingen niet meedelen. U mag uw oplossingen vanzelfsprekend vergelijken met die van andere studenten. Let echter ook daarbij op uw zoekmethode en redenering, en niet alleen op de oplossing zelf.
Documenten
Klik met de rechter muisknop op het document en kies "bewaren als". Daarna kan je het sneller bekijken of printen dan vanuit de browser.
-
regels vs. semantiek
Als je hier klikt kom je bij een bestand met een grote hoeveelheid theoretische vragen over de stof van Logica I.
Al wie Logica II volgt, zou daarop vlot moeten kunnen antwoorden. Dit is belangrijk voor je inzicht in de stof van Logica II en dus ook voor het examen.
Taalschema’s
Geef de precieze formulering van het taalschema voor elk van de volgende logica’s.
-
de modale logica K
-
de modale logica S4
-
de relevante logica E
-
de intuïtionistische logica IPC
Semantische clausules voor enkele ongewone connectieven
Hierna vindt u enkele connectieven, samen met hun betekenis in het Nederlands of de inferentieregels die ze definiëren. Formuleer voor elk ervan de semantische clausule (en ja, enkele ervan komen bekend voor).
| N |
A noch B |
| O |
A of B, maar niet beide |
| ! |
niet A of niet B |
| o |
A of B of beide |
| Z |
A of niet B |
| z |
A zowel als B |
| I |
A indien B |
| t |
A tenzij B |
| Y |
het is niet zo dat A of B |
| ô |
AôB / ~A
AôB / ~B
~A, ~B / AôB |
Enkele oefeningen over de metatheorie van PC
In de oefeningen wordt verwezen naar de propositionele fragmenten van de intuïtionistische logica IPC en de paraconsistente logica CLuN (PI). Toch zijn deze oefeningen erop gericht uw inzicht te verbeteren in de bewijstechnieken uit de metatheorie van de klassieke logica en in hun veralgemeenbaarheid naar verwante logica’s.
-
Toon aan dat het regelsysteem (analoog aan PIC1) voor de logica CLuN klopt met het axiomatisch systeem. (Beide richtingen.)
-
Maak een lijst van de lemma’s en theorema’s die we gebruiken om Theorema 12 te bewijzen. Doe, achterwaarts werkend, hetzelfde voor elk theorema en lemma in de lijst. Maak een overzichtelijke stamboom.
-
Gebruik het resultaat van 2 om het bewijs van de correctheid en volledigheid van PC aan te passen voor CLuN. Ga voor elk van de benodigde lemma’s en theorema’s na hoe ze (eventueel) moeten worden aangepast met betrekking tot de syntaxis en semantiek van CLuN.
Deze oefening oplossen vergt meerdere uren werk. Verdeel het eventueel over verschillende dagen.
-
Ga na hoe andere elementen van de metatheorie van PC kunnen worden aangepast voor CLuN. Voorbeeld: het bewijs dat de tableaumethode een beslissingsmethode is voor deze logica.
-
In lemma’s 3 en 4 wordt een meer klassieke weg gevolgd om theorema 12 te bewijzen. Kan deze weg worden aangepast voor CLuN? Zo ja, doe het dan even. Zo neen, waarom niet?
-
Voor de intuïtionistische oordeelslogica IPC wordt in het Logicaboek geen semantiek vermeld. Toch zijn er enkele metatheoretische eigenschappen van IPC die je gemakkelijk kan aantonen door te letten op de relatie tussen IPC en PC. Ga dit na.
-
Zij
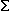 een verzameling van schematische letters voor zinnen (p, q, r, ...). Is er een valuatiefunctie die aan alle leden van
een verzameling van schematische letters voor zinnen (p, q, r, ...). Is er een valuatiefunctie die aan alle leden van 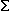 de waarde 1 toekent en aan alle andere schematische letters voor zinnen de waarde 0? Kunt u dat aantonen?
de waarde 1 toekent en aan alle andere schematische letters voor zinnen de waarde 0? Kunt u dat aantonen?
-
Maak een alternatief bewijs voor Lemma 1 door als volgt te vertrekken. Zij v een valuatiefunctie die aan alle schematische letters die lid zijn van
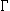 de waarde 1 toekent en aan alle andere schematische letters de waarde 0. Toon aan dat v aan alle leden van
de waarde 1 toekent en aan alle andere schematische letters de waarde 0. Toon aan dat v aan alle leden van 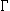 de waarde 1 toekent en aan alle andere formules de waarde 0. Is hiermee het bewijs afgelopen?
de waarde 1 toekent en aan alle andere formules de waarde 0. Is hiermee het bewijs afgelopen?
Geldigheid in het propositioneel fragment van de paraconsistente logica CLuN (PI)
Ga voor elk van de volgende wffs na of ze al dan niet geldig zijn in deze logica. Leg telkens uit waarom dit zo is.
-
~A
 (B
(B ~A)
~A)
-
~(A&~A)
 (A
(A ~A)
~A)
-
A
 (A
(A B)
B)
-
(A
 B)
B) A
A
-
(~A
 A)
A) A
A
-
B
 (~A
(~A ~A)
~A)
-
(~A
 B)
B) ~A
~A
-
~A
 (B
(B ~A)
~A)
-
~(A&~A)
 (A
(A ~A)
~A)
-
(A
 A)
A) B
B
-
(B
 ~A)
~A) ~A
~A
-
~(A&~A)
 (B
(B ~B)
~B)
-
~A
 (A
(A A)
A)
-
(~A
 A)
A) ~A
~A
-
~A
 (B
(B ~A)
~A)
-
(A
 ~A)
~A) ~(A&~A)
~(A&~A)
-
~A
 (B
(B ~A)
~A)
-
(~A
 A)
A) A
A
-
(A&~A)
 (A
(A ~A)
~A)
-
A
 ~~A
~~A
-
~(A&~A)
-
(A&~A)
 (A
(A B)
B)
-
A
 (~A
(~A A)
A)
-
~~A
 A
A
-
A
 (~B
(~B A)
A)
-
~A
 ~A
~A
-
(A
 B)
B) (~B
(~B ~A)
~A)
-
A
 (B
(B ~B)
~B)
-
(A&~A)
 (B
(B ~B)
~B)
-
~(A
 B)
B) ~A
~A
-
(A&~A)
 B
B
-
~(A&~A)
 ~(~A&A)
~(~A&A)
-
(A&~A)
 (A
(A B)
B)
-
((A
 B)&~A)
B)&~A) B
B
-
(~A
 ~B)
~B) (B
(B A)
A)
-
((A
 B)&~B)
B)&~B) ~A
~A
-
(A
 B)
B) (~A
(~A B)
B)
-
~(A
 B)
B) A
A
-
~(A
 B)
B) ~B
~B
Geldigheid in het propositioneel fragment van de paravolledige logica CLaN
De semantiek voor het propositioneel fragment van CLaN wordt uit de PC-semantiek bekomen door SPC5 te vervangen door “Als v(A) = 1, dan v(~A) = 0”.
Zijn de volgende wffs al dan niet geldig? Leg telkens uit waarom.
-
~A
 (B
(B ~A)
~A)
-
~(A&~A)
 (A
(A ~A)
~A)
-
A
 (A
(A B)
B)
-
(A
 B)
B) A
A
-
(~A
 A)
A) A
A
-
B
 (~A
(~A ~A)
~A)
-
(~A
 B)
B) ~A
~A
-
~A
 (B
(B ~A)
~A)
-
~(A&~A)
 (A
(A ~A)
~A)
-
(A
 A)
A) B
B
-
(B
 ~A)
~A) ~A
~A
-
~(A&~A)
 (B
(B ~B)
~B)
-
~A
 (A
(A A)
A)
-
(~A
 A)
A) ~A
~A
-
~A
 (B
(B ~A)
~A)
-
(A
 ~A)
~A) ~(A&~A)
~(A&~A)
-
~A
 (B
(B ~A)
~A)
-
(~A
 A)
A) A
A
-
(A&~A)
 (A
(A ~A)
~A)
-
A
 ~~A
~~A
-
~(A&~A)
-
(A&~A)
 (A
(A B)
B)
-
A
 (~A
(~A A)
A)
-
~~A
 A
A
-
A
 (~B
(~B A)
A)
-
~A
 ~A
~A
-
(A
 B)
B) (~B
(~B ~A)
~A)
-
A
 (B
(B ~B)
~B)
-
(A&~A)
 (B
(B ~B)
~B)
-
~(A
 B)
B) ~A
~A
-
(A&~A)
 B
B
-
~(A&~A)
 ~(~A&A)
~(~A&A)
-
(A&~A)
 (A
(A B)
B)
-
((A
 B)&~A)
B)&~A) B
B
-
(~A
 ~B)
~B) (B
(B A)
A)
-
((A
 B)&~B)
B)&~B) ~A
~A
-
(A
 B)
B) (~A
(~A B)
B)
-
~(A
 B)
B) A
A
-
~(A
 B)
B) ~B
~B
Tableaumethoden voor eenvoudige propositionele logica’s
-
Ontwerp een tableaumethode voor het propositioneel fragment van CLuN.
-
De semantiek van het propositioneel fragment van de paravolledige logica CLaN wordt hierboven uiteengezet. Ontwerp er een tableaumethode voor.
-
Het propositioneel fragment van de logica CLoN wordt bekomen door geen enkele beperking op te leggen op de waarde van formules van de vorm ~A. Ontwerp er een tableaumethode voor. Ziet u een systeem in wat in die logica nog geldt?
-
In de drie voorgaande logica’s wijkt de negatie af van de betekenis die ze heeft in PC. Is het mogelijk analoge afwijkingen in te voeren voor de andere connectieven? Probeer het eens met tableaumethoden.
Enkele vragen over modale logica’s
-
Ga voor elk van de volgende formules na in welke modale logica’s ze geldig zijn. Begin daartoe (zoals ik dat in de les deed) met een tableau in K. Als dat tableau niet sluit ga je na welke eigenschappen van de bereikbaarheidsrelatie nodig zijn om het te doen sluiten. Sommige formules zijn geldig in K, sommige in een van de andere behandelde systemen, sommige in geen enkel. Tracht eerst intuïtief te raden in welk systeem een formule geldig is.
-

 A
A
 A
A
-
(
 A&
A& (A
(A B))
B))
 B
B
-
A

 A
A
-
 (A
(A B)
B) (
( A
A
 B)
B)
-
 A
A

 A
A
-

 A
A A
A
-
(
 A&
A& (A
(A B))
B))
 B
B
-
Er zijn veel soorten modaliteiten. Tot de bekendste alethische modaliteiten behoren de logische, de nomologische en de technische. Gebruik de semantiek van de modale logica’s om te tonen dat deze respectievelijk overeenkomen met S5, S4 en T.
-
Stel dat we de modaliteit “X weet dat p” schrijven als
 p en de modaliteit “het is compatibel met alles wat X weet dat p” schrijven als
p en de modaliteit “het is compatibel met alles wat X weet dat p” schrijven als  p. Welke van de modale systemen is meest geschikt om de betekenis van deze kennismodaliteiten vast te leggen? Zie je ook bij dat systeem nadelen?
p. Welke van de modale systemen is meest geschikt om de betekenis van deze kennismodaliteiten vast te leggen? Zie je ook bij dat systeem nadelen?
-
Bij de deontische interpretatie van de modaliteiten lezen we
 p als “p is verplicht” en
p als “p is verplicht” en  p als “p is toegelaten”. Bepaal zelf “p is verboden”.
p als “p is toegelaten”. Bepaal zelf “p is verboden”.
-
Morele modaliteiten hebben een andere logische structuur dan juridische modaliteiten of, bijvoorbeeld, modaliteiten die bij een kaartspel horen (voorbeeld: bij het kaartspel bieden moet je volgen als je dan kan). Welke modale logica legt de betekenis vast van morele modaliteiten? Welke eigenschappen vallen in elk geval weg bij bijvoorbeeld verplichtingen en toelatingen die op een kaartspel slaan?
Opmerking. Er zijn heel wat paradoxen in de deontische logica. De meeste komen daaruit voort dat (i) bijna alle morele normen uitzonderingen hebben en (ii) bijna alle mensen morele normen aanvaarden die uit verschillende (en onvolledige) normensystemen afkomstig zijn. Om deze oefening op te lossen is het in elk geval nuttig te weten dat  A betekent dat sommige toestanden van de werkelijkheid waarin A waar, is toegelaten zijn (en niet dat elke toestand van de werkelijkheid waarin A waar is, toegelaten is). Ga na dat
A betekent dat sommige toestanden van de werkelijkheid waarin A waar, is toegelaten zijn (en niet dat elke toestand van de werkelijkheid waarin A waar is, toegelaten is). Ga na dat  (A
(A B) afleidbaar is uit
B) afleidbaar is uit  A. Ga ook na waarom dit een paradox lijkt te zijn, maar er geen is onder de bovenstaande interpretatie.
A. Ga ook na waarom dit een paradox lijkt te zijn, maar er geen is onder de bovenstaande interpretatie.
Het theorema van Gödel
Historische context, methode die achter de bewijzen zit, ‘overeenkomst’ taal-metataal en haar betekenis, de bewijzen zelf, betekenis van de theorema's.
Er zijn allerlei inleidende teksten (waaronder twee van mezelf) die nuttig kunnen zijn. Zorg er echter voor dat je de tekst van Van Heijenoort begrijpt. Zorg er ook voor dat je de betekenis van de Theorema's door hebt, zowel met betrekking tot de wiskunde als (vooral) daarbuiten.
Naast de tekst van Van Heijenoort zijn er korte stukjes over 2e orde axiomatisering, niet-standaard modellen, (beslisbare en niet-triviale) inconsistente modellen en hun relatie met de klassieke rekenkunde, en de kennistheoretische betekenis.
Een van de middelen om na te gaan of je de theorema's begrijpt, bestaat erin na te gaan wat er mis is aan teksten waarin wordt aangetoond dat de theorema's fout zijn (of dat verwante bewijzen fout zijn, bijvoorbeeld het bewijs dat de reële getallen overaftelbaar zijn (Cantor's diagonaalmethode).
Op het internet vind je redeneringen waarin met opzet (terwille van het pedagogisch nut) fouten verwerkt zijn. Amusanter zijn de teksten van mensen die menen dat er echt fouten zitten in Gödel's bewijs (en in aanverwante bewijzen). Hierna volgen enkele mooie en nuttige voorbeelden. Als je zelf in dit opzicht nuttige teksten vindt op het internet, stuur me dan het adres met een woordje uitleg.
Voorbeeldvraag:
Gödels eerste theorema zegt dat er in de taal van de rekenkunde een formule A is, die geen stelling is van PA en waarvan de negatie evenmin een een stelling is van PA (waarin PA een axiomastelsel voor de rekenkunde is).
Kan je op dezelfde manier ook aantonen dat er in de taal van PL een formule A is, zodat noch A noch ~A een stelling is van PL. Zo ja, hoe verloopt het bewijs? Zo neen, leg uit waarom niet.
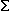 een verzameling van schematische letters voor zinnen (p, q, r, ...). Is er een valuatiefunctie die aan alle leden van
een verzameling van schematische letters voor zinnen (p, q, r, ...). Is er een valuatiefunctie die aan alle leden van 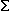 de waarde 1 toekent en aan alle andere schematische letters voor zinnen de waarde 0? Kunt u dat aantonen?
de waarde 1 toekent en aan alle andere schematische letters voor zinnen de waarde 0? Kunt u dat aantonen?
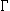 de waarde 1 toekent en aan alle andere schematische letters de waarde 0. Toon aan dat v aan alle leden van
de waarde 1 toekent en aan alle andere schematische letters de waarde 0. Toon aan dat v aan alle leden van 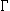 de waarde 1 toekent en aan alle andere formules de waarde 0. Is hiermee het bewijs afgelopen?
de waarde 1 toekent en aan alle andere formules de waarde 0. Is hiermee het bewijs afgelopen?
 (B
(B ~A)
~A)

 A
A